
sin A = opposite/hypotenuse = a/c
cos A = adjacent/hypotenuse = b/c
tan A = opposite/adjacent = a/b
We also note that:
sin A/cos A = (opposite/hypotenuse)/(adjacent/hypotenuse) = (a/c)*(c/b) = a/b = tan A
The important idea here is that regardless of the size of the right triangle, for the same angle, the ratio between the sides is the same. This follows directly from Euclid's theorem on equiangular triangles (see here). For those interested in the history of the terms of trigonometry (see here).
Unfortunately, defining sine and cosine by right triangles does not help us for angles greater than 90 degrees or for negative values. By convention, the definitions of sine and cosine have been generalized using a unit circle definition (that is, a circle where the radius is equal to 1 unit). This works out because at all angles of the circle, it is possible to generate a unique right angle (see here for demonstration).
Consider a circle which has the radius r = 1.
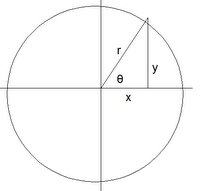
We now define sine and cosine such that:
sin θ = y/r
cos θ = x/r
Where θ is between 0 and 90 degrees, this forms a right triangle and gives values consistent with the right triangle definitions above. This unit circle definition has the following additional properties:
Property 1: sin(0 degrees) = 0 and sin(180 degrees) = 0
Since at 0 degrees and at 180 degrees, y = 0.
Property 2: sin 90 degrees = 1
Since at 90 degrees, y = r.
Property 3: if θ is greater than 90 degrees and θ is less than 180 degrees, sin θ = sin(180 - θ)
Since sin is a ratio of y/r (independent of x) and since 180 - θ forms a symmetrical angle with the same value of y. See below for proof:
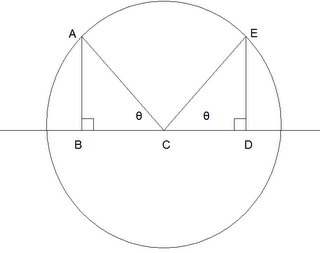
Proof:
(1) We can see that triangle ABC ≅ to triangle EDC by Angle-Angle-Side (see here) since: θ ≅ θ, AC and EC are both radii of unit length, and ∠ ABC and ∠ EDC are right angles.
(2) So therefore AB ≅ ED which shows that y is the same for ∠ θ and ∠ 180 - θ .
QED
Property 4: sin (-θ) = -sin θ
For a negative value of θ, y has a negative value but is otherwise symmetrical with the positive value. See below for proof:

Proof:
(1) We can see that triangle CED ≅ CFD by Angle-Angle-Side (see here) since CF, CE are radii of 1 unit, ∠ EDC and FDC are right angles; θ ≅ θ.
(2) So, we can see that ED ≅ DF even if DF represents a negative value of y and ED represents a positive value of y.
QED
Property 5: sin (θ + 360 degrees) = sin θ and cos(θ + 360 degrees) = cos θ
This is clear since we are using a circle as our definition and a circle consists of 360 degrees. This follows directly from our postulate of a line as having 180 degrees (see here).
Proof:
(1) Divide an circle in half with a straight line (for example, see the figure above).
(2) All the angles along the top of the line will add up to 180 degrees and likewise all the angles along the bottom will add up to 180 degrees since a straight line totals 180 degrees. (see here)
(3) Since a circle consists of the sum of top angles and the bottom angles, we can see that a circle consists of 360 degrees.
QED
Property 6: cos(0 degrees) = 1 and cos(180 degrees) = -1
This is true since at 0 degrees, x = r and at 180 degrees, -x = r.
Property 7: cos 90 degrees = 0
This is true since at 90 degrees, x = 0.
Property 8: if θ is greater than 90 degrees and less than 180 degrees, then cos θ = -cos (180 - θ)
This is true since in these cases x is negative and has a value symmetrical with the 180 - θ . This is the same as the proof for Property 3 above. It is negative since even though BC ≅ CD, BC corresponds to a negative value of x while CD corresponds to a positive value of x.
QED
Property 9: cos (-θ) = cos θ
This is true since in both the positive and negative θ cases, x still has the same value and cos is independent of y. This is the same proof as Property 4. From this proof we see that both angles involve the same positive value of x as represented by CD.
QED
It is the unit circle definition which gives us the familiar graph of sine and cosine waves (see here for details on how the unit circle provides this graph):

This is all well and good but they rely on Euclidean geometry. It turns out that using the Taylor Series (see here) from calculus, it is possible to derive an equation for sine and cosine which are independent of any assumptions from Euclid. Here they are:
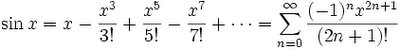

tan x = sin x/cos x
For those interested in understanding how the Taylor Series can be used to derive these equations, see here.
It turns out that with these equations, we arrive at one of the most astounding equations in all of mathematics, Euler's Formula (see here):
eix = cosx + isinx
I talk more about this equation in the context of Fermat's Last Theorem here.
References:
- Trigonometric Functions, Wikipedia