Postulate 1: The distance d between two points (x1,x2) and (y1,y2)
d = √(x2 - x1)2 + (y2 - y1)2
This postulate assumes all the postulates from Euclid but that works fine for the standard Cartesian coordinates.
Definition 1: A circle
A circle is the set of points equidistant from a given point. This given point is called the center. The distance from the center to any point in the set of points is called the radius.
Theorem 1: Equation of a circle
For any given circle with center at (centerX, centerY) and radius r, the equation is:
(x - centerX)2 + (y - centerY)2 = r2
Proof:
(1) By Definition 1 above and Postulate 1 above, we have:
r = √(x - centerX)2 + (y - centerY)2
(2) Squaring both sides gives us:
r2 = (x - centerX)2 + (y - centerY)2
QED
Tuesday, January 08, 2008
Monday, January 07, 2008
Geometric Interpretation of Roots of Unity
The nth roots of unity can be thought of as n points evenly dividing up a circle.
Wolfram's MathWorld web site has a wonderful graphic that demonstrates this:

Here's the reason that it's true:
Theorem: The N-th Roots of Unity correspond to n points evenly dividing up a circle
Proof:
(1) The number of radians in a circle is 2π [See here for review of radians, if needed]
(2) The equation for roots of unity is (see Corollary 1.1, here):

where 0 ≤ k ≤ n-1.
(3) So each root of unity is:
cos[ (2kπ)/n] + isin[(2kπ)/n]
where 0 ≤ k ≤ n-1
(4) Which is the same as:
cos[(k/n)2π] + isin[(k/n)2π]
where 0 ≤ k ≤ n -1
(5) Now, complex values can be graphed on the Cartesian coordinate system on x + iy [this is called the complex plane].
(6) Each of the roots above maps to a point on the circumference of a unit circle since:
(a) The equation for a unit circle at (0,0) is [See Theorem 1, here]:
x2 + y2 = 1
(b) Since we are mapping cos[(k/n)2π] + isin[(k/n)2π] to x + iy, this gives us:
x = cos[(k/n)2π]
y = sin[(k/n)2π]
(c) From a previous result (see Corollary 2, here), we have:
cos2[(k/n)2π] + sin2[(k/n)2π] = 1
(d) So, applying step #6b above gives us:
x2 + y2 = 1
(7) So, all we have left to prove is that each of these n points is equidistant from the adjacent points on the circle.
(8) Clearly, we have points at based on the following n values:
(0/n)2π, (1/n)2π, (2/n)2π, ..., [(n-1)/n]2π
where
y = cos[(k/n)2π]
x = sin[(k/n)2π]
(9) Now, if we use a unit circle, it is clear that each of these points is equidistant from each other since:
Consider a circle which has the radius r = 1.
It is clear that plotting lines at (0/n)2π, (1/n)2π. ... ([n-1]/n)2π divides up the total circle (2π radians) into n equal portions.
Using a unit circle, it is clear that x=[cos(k/n)2π] and y = [sin(k/n)2π] are the places of intersection when the circle is evenly divided since:
sin θ = y/r = y
cos θ = x/r = x
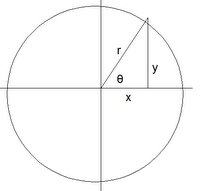
In other words, each y=cos[(k/n)2π] and x=sin[(k/n)2π] is a point at the place where the (k/n)th part of the circle sweeps out against the circumference of the circle.
Since the length of the circumference is πD=(2r)πr = 2(1)π, [see Corollary 1, here], this means that the length of each subtended arc is (k/n)*2π.
This results in the patterns above depending upon the value of n.
QED
For example, if we graph the third roots of unity. Then, we have:
lines sweeping out at:
0, (1/3)2π, and (2/3)2π.
which results in the following graph:

References
Wolfram's MathWorld web site has a wonderful graphic that demonstrates this:

Here's the reason that it's true:
Theorem: The N-th Roots of Unity correspond to n points evenly dividing up a circle
Proof:
(1) The number of radians in a circle is 2π [See here for review of radians, if needed]
(2) The equation for roots of unity is (see Corollary 1.1, here):

where 0 ≤ k ≤ n-1.
(3) So each root of unity is:
cos[ (2kπ)/n] + isin[(2kπ)/n]
where 0 ≤ k ≤ n-1
(4) Which is the same as:
cos[(k/n)2π] + isin[(k/n)2π]
where 0 ≤ k ≤ n -1
(5) Now, complex values can be graphed on the Cartesian coordinate system on x + iy [this is called the complex plane].
(6) Each of the roots above maps to a point on the circumference of a unit circle since:
(a) The equation for a unit circle at (0,0) is [See Theorem 1, here]:
x2 + y2 = 1
(b) Since we are mapping cos[(k/n)2π] + isin[(k/n)2π] to x + iy, this gives us:
x = cos[(k/n)2π]
y = sin[(k/n)2π]
(c) From a previous result (see Corollary 2, here), we have:
cos2[(k/n)2π] + sin2[(k/n)2π] = 1
(d) So, applying step #6b above gives us:
x2 + y2 = 1
(7) So, all we have left to prove is that each of these n points is equidistant from the adjacent points on the circle.
(8) Clearly, we have points at based on the following n values:
(0/n)2π, (1/n)2π, (2/n)2π, ..., [(n-1)/n]2π
where
y = cos[(k/n)2π]
x = sin[(k/n)2π]
(9) Now, if we use a unit circle, it is clear that each of these points is equidistant from each other since:
Consider a circle which has the radius r = 1.
It is clear that plotting lines at (0/n)2π, (1/n)2π. ... ([n-1]/n)2π divides up the total circle (2π radians) into n equal portions.
Using a unit circle, it is clear that x=[cos(k/n)2π] and y = [sin(k/n)2π] are the places of intersection when the circle is evenly divided since:
sin θ = y/r = y
cos θ = x/r = x

In other words, each y=cos[(k/n)2π] and x=sin[(k/n)2π] is a point at the place where the (k/n)th part of the circle sweeps out against the circumference of the circle.
Since the length of the circumference is πD=(2r)πr = 2(1)π, [see Corollary 1, here], this means that the length of each subtended arc is (k/n)*2π.
This results in the patterns above depending upon the value of n.
QED
For example, if we graph the third roots of unity. Then, we have:
lines sweeping out at:
0, (1/3)2π, and (2/3)2π.
which results in the following graph:

References
- Rowland, Todd and Weisstein, Eric W. "Root of Unity." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RootofUnity.html
- "Complex Plane", Wikipedia.com
- "Roots of Unity", Wikipedia.com
Subscribe to:
Comments
(
Atom
)