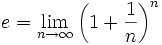Parallel Lines

In today's blog, I review some basic ideas of parallel lines. I will later use these proofs to establish the basic properties of sin and cosin functions.

Postulate 1: The angles of a straight line add up to 180 degrees.

Lemma 1: Vertical angles are congruent

Let AB and EF be two lines that intersect at E.












Then:

∠ EGB ≅ ∠ AGF

Proof:

(1) ∠ EGB + ∠ EGA = 180 degrees. [Postulate 2]

(2) ∠ EGA + ∠ AGF = 180 degrees.

(3) So ∠ EGB = 180 - ∠ EGA and ∠ AGF = 180 - ∠ EGA

(4) So, ∠ EGB ≅ ∠ AGF.

QED

Lemma 2: If any corresponding angles of an intersected line are congruent, then all corresponding angles are congruent.


















Proof:

(1) We start with ∠ EGA ≅ ∠ EHC

(2) Using Postulate 1, we know that ∠ EGB ≅ ∠ EHD since:
∠ EGA + ∠ EGB = 180 so that ∠ EGB = 180 - ∠ EGA
∠ EHC + ∠ EHD = 180 so that ∠ EHD = 180 - ∠ EHC

(3) Using Lemma 1, we get:
∠ FGA ≅ ∠ FHC since:
∠ FGA ≅ ∠ EGB and ∠ FHC ≅ ∠ EHD

∠ FGB ≅ ∠ FHD since:
∠ FGB ≅ ∠ EGA and ∠ FHD ≅ ∠ EHC

QED

Since any one corresponding angle implies the rest, we can use this as a definition for parallel lines.

Definition 1: Two lines are parallel if any and only if the corresponding angles of an intersecting line are congruent.

In the case of the example above, lines AB and CD are parallel if we can prove any of the following true:
(a) ∠ EGB ≅ ∠ EHD
(b) ∠ EGA ≅ ∠ EHC
(c) ∠ FHC ≅ ∠ FGA
(d) ∠ FHD ≅ ∠ FGB

Postulate 2: From any point not on a line, it is possible to construct a line that intersects the point and is parallel to the other line.

Lemma 3: Alternate angles of parallel lines are congruent

















Proof:

(1) ∠ AGF ≅ ∠ CHF [From Definition of Parallel Lines]

(2) ∠ CHF ≅ ∠ EHD [From Lemma 1: Verical Angles]

(3) ∠AGF ≅ ∠ EHD

QED

Lemma 4: The angles of a triangle add up to 180 degrees














Proof:

(1) Let EC be a line that is parallel AB [Postulate 2]

(2) ∠ ECA ≅ ∠ BAC [Lemma 3, Alternating angles of parallel lines]

(3) ∠ ECD ≅ ∠ ABC [Lemma 2, Corresponding angles of parallel lines]

(4) Now ∠ ACB + ∠ ECA + ∠ ECD = 180 degrees [Postulate 1]

(5) So ∠ ABC + ∠ BAC + ∠ ACB = 180 degrees too.

QED

References

• David Joyce, Euclid's Elements
  

Derivative of e

In today's blog, I will show the proof for the derivative of e and derivative of the natural logarithm.

Lemma 1: d/dx(ln x) = 1/x

Proof:

(1) d/dx(ln x) = lim (Δx → 0) (ln (x + Δ x) - ln x)/Δ x =
= lim (Δx → 0)(ln([x + Δx]/x)/Δ x [From the basic properties of logarithms, see here]

= lim(Δx → 0) (1/Δ x)(ln([x + Δx]/x) =

= lim (Δx → 0) (ln[([x + Δx]/x)^(1/Δx)])

= lim(Δx → 0) (ln[(1 + Δx/x)^(1/Δx)])

(2) Let u = Δx/x

(3) lim(Δx → 0) (ln[(1 + Δx/x)^(1/Δx)]) =
= lim (u → 0)(ln[(1 + u)^(1/[ux])]) =
= lim(u → 0)([1/x][ln(1 + u)^(1/u)])

(4) Now lim(u → 0) (1 + u)^(1/u) =
= lim(u → inf)(1 + 1/u)^u since:

(a) lim (u → inf)(1/u) = lim(u → 0)(u)

(b) lim (u → inf)(u) = lim (u → 0)(1/u)

(5) Now, (#4) is the definition of Euler's Number (see here), so we have:
lim(u → inf)(1 + 1/u)^(u) = e

which means that:

lim(u → 0)(1 + u)^(1/u) = e

(6) Putting (#5) in (#3) gives us:

lim(u → 0)([1/x][ln(1 + u)^(1/u)]) =
= (1/x)ln(e) = (1/x)(1) [Since ln e = 1, see here for definition of ln ]

QED

Lemma 2: (d/dx)e^x = e^x

Proof:

(1) Set u = e^x

(2) Using the chain rule we have:
(d/dx) ln u = (d/du)ln u * (d/dx)(e^x)

(3) From lemma 1, we know that:
(d/du)ln u = (1/u)

(4) We also know that:
(d/dx)(ln(e^x)) = (d/dx)(x) = 1

(5) So from #2, we get:
(d/du)ln u * (d/x)(e^x) = (1/u)(d/x)(e^x) = 1

(6) Or simply:
(1/u)(d/x)(e^x) = 1

(7) Multiplying u to both sides gives us:
(d/x)(e^x) = u

(8) But u = e^x, so we get:
(d/x)(e^x) = e^x

QED

References:

• (d/dx)ln x, math.com
• (d/dx)e^x,math2.org
  

Logarithms

Each elementary mathematical operation has an inverse operation that has the ability to cancel it. Subtraction and addition are inverses as are multiplication and division. From one perspective, n-roots are the inverse operation to exponents. If xⁿ = y, then x = ⁿ√y.

So that the inverse operation becomes:

ⁿ√xⁿ = x.

But what about the value n? Can we do an operation on n which cancels out x? The answer is yes, with logarithms.

In logarithms, we say that log_x y = n. So from this perspective, a logarithm is an inverse of the power operation in the sense that:

x^{log_x y} = y

This concept of logarithms and methods for deriving them were first popularized in the west by John Napier in 1614. Historically, logarithms were handled using logarithm tables. For those interested in the history of logarithms and logarithm tables, Wikipedia has an excellent article here.

One of the most important logarithm functions in log_e which is written as ln. This turns out to have very important mathematical properties such as:

∫(1/x)dx = ln x

Here are some very basic properties of logarithms that I use in other proofs:

Lemma 1: log_x a + log_x b = log_x (ab)

Proof:

(1) Let a,b be any two real, nonzero numbers.

(2) Let a' = log_x a so that a = x^(a')

(3) Let b' = log_x b so that b = x^(b')

(4) Now x^(a')*x^(b') = x^{(a' + b')} [See here for review of exponents if needed]

(5) So (ab) = x^{(a' + b')} [From #4]

(6) So log_x (ab) = a' + b' = log_x a + log_x b

QED

Lemma 2: log_x a - log_x b = log_x (a/b)

Proof:

(1) Let a,b be any two real, nonzero numbers.

(2) Let a' = log_x a so that a = x^(a')

(3) Let b' = log_x b so that b = x^(b')

(4) Now x^(a')/x^(b') = x^{(a' - b')} [See here for review of exponents if needed]

(5) So (a/b) = x^{(a' - b')} [From #4]

(6) So log_x (a/b) = a' - b' = log_x a - log_x b

QED

Lemma 3: b*log_x a = log_x (a^b)

Proof:

(1) Let a,b be any two real, nonzero numbers.

(2) b*log_x a = log_x a + ... + log_x a [So that we have b items to add together]

(3) From (#2) and Lemma 1 above, we have
b*log_x a = log_x a + ... + log_x a = log_x (a*a*...*a)

(4) Since we have b multiples of a, we get:
b*log_x a = log_x (a^b)

QED

References

• Logarithms, Wikipedia
  

Euler's Number

In 1683, Jacob Bernoulli was working on a problem with regard to compound interest. In calculating compound interest, the formula comes down to (1 + 1/n)ⁿ. Bernoulli noticed that this equation had a limit between 2 and 3 as n got larger and larger.

Today, we would state the definition for Euler's Number in the following way:


so that:

e = 2.7182...

This value is called Euler's Number after Leonhard Euler. Euler refered to the constant as "e" in 1727. He was not the first to discover the constant but he published so many important mathematical works relating to e that it became known as Euler's Number. Interestingly, it is believed that Euler chose "e" not because it was the first letter of his last name but because he wanted to use a vowel and he had already used "a".

Here is a graph of e^x:



References

• History of e, MacTutor
• e, Wikipedia
  

Generalized Power Rule

In today's blog, I continue review of the basics of calculus and derivatives. Today, I will go over the Generalized Power Rule for Derivatives.

This rule can be used in the the proof for Taylor's Formula.

Lemma 1: The Root Rule

dy/dx(x^(1/q)) = (1/q)x^(1/q)-1

Proof:

(1) Let y = x^(1/q)

(2) Then, x = y^q

(3) dx/dy(y^q) = qy^q-1 [From the Power Rule, see here]

(4) dy/dx = 1/(dx/dy) = 1/(qy^q-1)

(5) Applying (#1) to (#4) gives us:

dy/dx = 1/(q[x^(1/q))^q-1]) =
= (1/q)(1/[x^{1 - (1/q)}]) =
= (1/q)(x^(1/q)-1)

QED

Lemma 2: The Chain Rule

If a function f is differentiable at x and a function g is also differentiable at f(x), then if h is a function such that h(x) = g(f(x)), then h'(x) = g'(f(x))*f'(x)

Proof:

(1) Let x₀ be a point where f is differentiable.

(2) Let y₀=f(x₀) and be a point where g is differentiable.

(3) Let k(Δx) = f(x₀ + Δx) - f(x₀) where Δx is nonzero and k(Δx) is nonzero.

(4) Then:

[g(f(x₀ + Δx)) - g(f(x₀))]/Δx =

= [[g(f(x₀) + k(Δx)) - g(f(x₀))]/k(Δx)]*[(k(Δx)/Δx]

(5) Let's define a function φ such that:


(6) We can see that φ is continuous at k=0 since differentiability implies continuity (see Lemma 4 here)

(7) So, from (3), we see that:
lim (k → 0) φ(k) = g'(f(x₀)).

(8) Now, lim(Δx → 0) k(Δx) = lim(Δx → 0)[f(x₀ + Δx) -f(x₀)] = f(x₀)-f(x₀) = 0

(9) Because f is continuous at x₀ and because φ(0) = g'(f(x₀)), we conclude from (#5):

lim (Δx → 0) φ(k(Δx)) = g'(f(x₀))

(10) Applying #5 to #4 gives us
[[g(f(x₀) + k(Δx)) - g(f(x₀))] /k(Δx)]*[k(Δx)/Δx] = φ(k(Δx))*[k(Δx)/Δx]

(11) Applying #3 to #10 gives us
φ(k(Δx))*[k(Δx)/Δx] = φ(k(Δx))*[[f(x₀ + Δx) - f(x₀)]/(Δ x)]

(12) Using #4 thru #11 gives us:

lim (Δx → 0) [g(f(x₀ + Δx)) - g(f(x₀))]/Δ x =

= lim (Δ x → 0) φ(k(Δx))*[f(x₀ + Δx) - f(x₀)]/Δ x =

= g'(f(x₀))*f'(x₀)

QED

Corollary: if n is an integer, then D[f(x)]ⁿ = n[f(x)]^n-1f'(x)

(1) Let g(u) = uⁿ where n is an integer

(2) g'(u) = nu^n-1 [By the Power Rule for Derivatives, see here]

(3) Now, if u = f(x), then g'(u) = g'(f(x))*f'(x) [From Chain Rule above]

(4) So, D[f(x)]ⁿ/dx = n[f(x)]^n-1*f'(x) [From #2 and #3]

QED

Theorem: Generalized Power Rule

If x is differentiable at x and r is a rational number, then:
D([f(x)^r])/dx = r[f(x)]^r-1*f'(x)

Proof:

(1) [f(x)]^(p/q)] = {[f(x)]^p}^(1/q) = u^(1/q) where p,q are positive integers and u = [f(x)]^p

(2) Du/dx = p[f(x)]^p-1f'(x) [From the Corollary above]

(3) D[f(x)]^(p/q)/dx = Du^(1/q)/dx =

= (1/q)u^(1/q)-1Du/dx [From the Root Rule above]

= (1/q){[f(x)]^p}^(1/q)-1p[f(x)]^p-1f'(x) [From step # 2 above]

= (p/q)[f(x)]^{p((1/q)-1)+p-1}f'(x)

= (p/q)[f(x)]^(p/q)-1f'(x)

QED

References

• Edwards & Penny, Calculus and Analytic Geometry