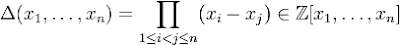A polynomial invariant on all but one variable

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Lemma:

Let g be a polynomial in n indeterminates x₁, ..., x_n over some field K.

Let g be invariant under every permutation of x₂, ..., x_n

Then:

g can be written as a polynomial in x₁ and the elementary symmetric polynomials s₁, ..., s_n-1 in x₁, ..., x_n

Proof:

(1) We can view g as a polynomial in x₂, ..., x_n with coefficients in K[x₁].

(2) Using Waring's Method [see Theorem 4, here], we know that g can be written as a polynomial in the elementary symmetric polynomials s'₁, ..., s'_n-1 in x₂, ..., x_n with coefficients in K[x₁]

(3) Therefore, there exists a polynomial g' such that:

g(x₁, ..., x_n) = g'(x₁, s'₁, ..., s'_n-1)

where:

s'₁ = x₂ + ... + x_n

s'₂ = x₂x₃ + ... + x_n-1x_n

...

s'_n-1 = x₂*...*x_n

(4) To complete the proof, we need to show that s'₁, s'₂, ..., s'_n-1 can be restated in terms of s₁, s₂, ..., s_n where:

s₁ = x₁ + ... + x_n

s₂ = x₁x₂ + ... + x_n-1x_n

...

s_n = x₁*...*x_n

(5) We know that for any given polynomial [see Theorem 1, here]:

(X - x₁)*...*(X - x_n) = Xⁿ - s₁X^n-1 + ... + (-1)ⁿs_n

(6) Now, we can use the same principle to get:

(X - x₂)*...*(X - x_n) = X^n-1 - s'₁X^n-2 + ... + (-1)^n-1s'_n-1

(7) Multiplying the above equation by (X - x₁) gives us:

(X - x₁)*...*(X - x_n) = (X - x₁)X^n-1 - (X - x₁)s'₁X^n-2 + ... + (X - x₁)(-1)^n-1s'_n-1 =

Xⁿ - (x₁+s'₁)X^n-1 + (x₁s'₁ + s'₂)X^n-2 - (x₁s'₂ + s'₃)X^n-3 + ... + (-1)ⁿ(x₁s'_n-1)

(8) Combining step #5 and step #7 gives us:

s₁ = x₁ + s'₁

so that:

s'₁ = s₁ - x₁


s₂ = x₁s'₁ + s'₂

so that:

s'₂ = s₂ - x₁s'₁ = s₂ - x₁(s₁ - x₁) = s₂ - x₁s₁ + x₁²

and so on...

(9) Since we can subtitute all values s'_i in terms of x₁ and s₁, ..., s_n, we can use the equation in step #3 to get:

g(x₁, ..., x_n) = g'(x₁, s'₁, ..., s'_n-1) = g'(x₁, s₁ - x₁, s₂ - s₁x₁ + x₁², ... )

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Nonzero Polynomials with Distinct Parameters

The following is taken from Harold M. Edwards in his book Galois Theory.

Theorem:

Let K be a field.

Let x₁, x₂, x₃, ... be an infinite sequence of distinct elements of K

Let f(A,B,C,...) be a nonzero polynomial in n variables A,B,C,... with coefficients in K

Then:

It is possible to select values A=x_j, B = x_k, C = x_m for the variables A,B,C from the sequence x₁, x₂, x₃, ... so that F( x_j, x_k, x_m, ...) ≠ 0

Proof:

(1) Assume that f(x) is a nonzero polynomial of one variable with degree m.

(2) Using the Fundamental Theorem of Algebra (see Theorem, here), we know that f(x) has at most m distinct roots.

(3) If we list off m+1 distinct elements of K from the infinite sequence, it is clear that at least one (let us say x_r) will not be a root.

(4) So that f(x_r) ≠ 0

(5) Assume that this is true up to n-1 variables for F(A,B,C...,Y) so that we know that F(x_i, x_j, ..., x_y) ≠ 0

(6) Let G be a function of n variables so that we have G(A,B,C,...Z)

(7) Let H be a function on the first n-1 variables so that we have H(A,B,C,...Y) = G(A,B,C,...,Y,1)

(8) By assumption, we can find x_i, x_j, ... x_y such that:

H(x_i, x_j, ..., x_y) ≠ 0

(9) But then G(x_i, x_j, ..., x_y, 1) ≠ 0.

QED

References

• Harold M. Edwards, Galois Theory, Springer, 1984

Products of Nonzero Polynomials

The following is taken from Harold M. Edwards in his book Galois Theory.

Theorem: The product of nonzero polynomials is a nonzero polynomial

Proof:

(1) This theorem is clearly true in the case of one nonzero polynomial.

(2) Let's assume that it is true up to p-1.

(3) So that the product of p-1 nonzero polynomails is a nonzero polynomial g(x) of degree n so that we have:

g(x) = a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n

where a₀ is nonzero.

(4) Let us assume that f(x) is a nonzero polynomial of degree m so that:

f(x) = b₀x^m + b₁x^m-1 + ... + b_m-1x + b_m

where b₀ is nonzero

(5) f(x)*g(x) is nonzero since:

the only term with degree m+n is a₀*b₀ which cannot be 0.

(6) So, by induction this proposition is true for all products.

QED

References

• Harold M. Edwards, Galois Theory, Springer, 1984

The Discriminant

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

For a definition of symmetric polynomials, see Definition 1, here.

Lemma 1:

Let


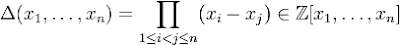
Then:

Δ(x₁, ..., x_n)² is a symmetric polynomial

Proof:

(1) Let P = ∏ (x_i - x_j)

(2) If any x_i = x_j, then P = 0. [that is, if there is a multiple root]

(3) Assume that there are no multiple roots.

(4) If we swap any two roots, then the result is either P or -P, then the result is to permute the ordering of each of the differences and to change the signs of some.

(5) Ordering doesn't change the product so the only the change that occurs is the sign of the product. That is, the result is P or -P depending upon which parameters get swapped.

(6) So it is clear that ∏ (x_i - x_j) is not symmetric.

(7) If we permutate the values of [∏ (x_i - x_j)]², it is clear that the result is always P² = P² = (-P)²

QED


Using Waring's Method (see Theorem 4, here), we know that [∏ (x_i - x_j)]² can be expressed as a function of the elementary symmetric polynomials (for review, see here) so that we have:

Definition 1: The Discriminant Δ

Let



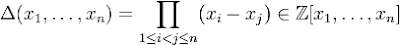
Then the Discriminant D is:

D(s₁, ..., s_n) = Δ(x₁, ..., x_n)²

where s₁, ..., s_n are the elementary symmetric polynomials.


Example 1: Discriminant of a generic polynomial of degree 2

D(s₁,s₂) = s₁² - 4s₂

First, we carry out the multiplication:

Δ(x₁,x₂)² = (x₁ - x₂)² = x₁² + x₂² - 2x₁x₂

Then, we show it as a function of the elementary symmetric polynomials:

x₁² + x₂² - 2x₁x₂ = (x₁ + x₂)² - 4x₁x₂=s₁² - 4s₂


Example 2: Discriminant of a generic polynomial of degree 3

D(s₁,s₂,s₃) = s₁²s₂² + 18s₁s₂s₃ - 27s₃² -4s₁³s₃ - 4s₂³

We note that:

Δ(x₁,x₂,x₃) = (x₁ - x₂)(x₁ - x₃)(x₂ - x₃)

We can simplify this by restating Δ(x₁,x₂,x₃) as:

Δ(x₁,x₂,x₃) = A - B

where:

A = x₁²x₂ + x₂²x₃ + x₃²x₁

and

B = x₁x₂² + x₂x₃² + x₃x₁²

So that:

Δ(x₁,x₂,x₃)² = (A - B)² = A² + B² - 2AB = (A + B)² - 4AB

Now, we note that A+B and AB are symmetric polynomials and using Waring's method (see Theorem 4, here), we have:

A + B = ∑ x₁²x₂ = s₁s₂ - 3s₃

AB = ∑ x₁⁴x₂x₃ + ∑ x₁³x₂³ + 3x₁²x₂²x₃² = s₁³s₃ + s₂³ - 6s₁s₂s₃ + 9s₃²

Now, we can combine these results to get the discriminant:

(A + B)² - 4AB = ( s₁s₂ - 3s₃)² - 4( s₁³s₃ + s₂³ - 6s₁s₂s₃ + 9s₃²) =

= s₁²s₂² + 18s₁s₂s₃ - 27s₃² -4s₁³s₃ - 4s₂³


Example 3: Discriminant of x³ + px + q

D(s₁,s₂,s₃) = -27q² - 4p³

First, we note that the values of the elementary symmetric polynomials can be derived from the coefficients of a polynomial (see Theorem 1, here) so that:

s₁ = 0

s₂ = p

s₃ = -q

So that:

s₁²s₂² + 18s₁s₂s₃ - 27s₃² -4s₁³s₃ - 4s₂³= 0 + 0 - 27(-q)² - 0 - 4p³ = -27q² - 4p³


Theorem 2:

Let P ∈ R[X] be a monic polynomial with real coefficients, which splits into a product of linear factors over C such that:

P = (x - u₁)*...*(x - u_n)

for some u₁, ..., u_n ∈ C.

Let d ∈ R be the discriminant of P

The equality d=0 holds if and only if P has a root of multiplicity at least 2 in C

If all the roots of P are real, then d ≥ 0. If n=2 or n=3 and not all the roots are real, then d ≤ 0.

Proof:

(1) d = ∏ (u_i - u_j)² where 1 ≤ i is less than j ≤ n

(2) If P has a root of multiplicity at least 2, then d = 0 since we have a case where u_i = u_j

(3) If all the roots are real, then d ≥ 0 since any real number squared is greater or equal to 0 and product of nonnegative numbers is greater or equal to 0.

(4) Assume n =2

(5) d = (u₁ - u₂)² [see Definition 1 above]

(6) If u₁ is not real, then u₂ = u₁ [see Theorem 5, here]

(7) Let u₁ = a + bi

(8) Let u₂ = a - bi

(9) (u₁ - u₂)² = (a + bi - [a - bi])² = (2bi)² = -4b² = -abs(4*b²)

(10) So that d ≤ 0.

(11) Assume that n = 3

(12) Then, d = (u₁ - u₂)²(u₁ - u₃)²(u₂ - u₃)²

(13) Assume that not all three roots are real. So, we can assume that u₁ is not real.

(14) Then, it follows that its conjugate is also a root. So we can assume that u₂ is not real and u₁ = u₂

(15) We know that u₃ is then real. [see Theorem 3, here]

(16) So there exists real numbers a,b,c such that:

u₁ = a + bi

u₂ = a - bi

u₃ = c

And we have:

(u₁ - u₂)(u₁-u₃)(u₂ - u₃) = [a+bi - (a - bi)][a+bi - c][a-bi - c] = (2bi)([a-c]+bi)([a-c]-bi)

Now, we know that:

([a - c] + bi)([a - c] - bi) = [a - c][a - c] - bi[a - c] + bi[a - c] - [bi][bi] =[a - c]² + b²

Combining this with the above we get:

(2bi)[(a - c)² + b²] = i[(2b)(a - c)² + 2b²]

Now, it is clear that (2b)(a - c)² + 2b² is a real number since a,b,c are real and we can set s = (2b)(a - c)² + 2b² where s is a real number.

So d = (is)² = -(s²) = -abs(s²)

(17) So, d ≤ 0.

QED

Corollary 2.1:

x³ + px +q = 0

has three distinct real solutions if and only if (p/3)³ + (q/2)² is less than 0.

Proof:

(1) By Exercise 3 above, the discriminant of x³ + px +q is d = -27q² - 4p³

We further note that:

d = -27q² - 4p³ = -2²3³[(p/3)³ + (q/2)²]

(2) Now if (p/3)³ + (q/2)² is less than 0, it follows that d ≥ 0.

(3) So, using Theorem 2 above, we are done.

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Irreducible Polynomials and Relatively Prime Polynomials

Lemma 1:

Let g(x) be an irreducible polynomial with coefficients in a field K

Let h(x) be a polynomial with coefficients in a field K.

If g(x) does not divide h(x), then g(x) and h(x) are relatively prime

Proof:

(1) Let d(x) be the greatest common denominator for g(x) and h(x). [see Theorem 1, here for proof of the existence of d(x)]

(2) Since g(x) is irreducible, this means that d(x) must be of degree 0 or of the same degree as g(x). [see Definition 1, here]

(3) Assume that degree d(x) is nonzero.

(4) Then it follows that g(x)=C*d(x) where C is a constant. [since d(x) is a divisor of g(x) and since deg d(x) = deg g(x).]

(5) But then [1/C]*g(x) is a divisor of h(x) since d(x) is a divisor of h(x).

(6) But this is impossible since g(x) does not divide h(x).

(7) So we have a contradiction and we reject our assumption in step #3 and conclude that deg d(x) is 0.

(8) But then this means that g(x) and h(x) are relatively prime. [see Definition 3, here]

QED