Countability

Definition 1: Set of natural numbers N

The set of natural numbers N = { 1, 2, 3, ... }

Definition 2: Set of integers Z

The set of integers Z = { .., -2, -1, 0, 1, 2, ... }

Definition 3: Set of rational numbers Q

The set of rational numbers Q = { a/b : where a,b ∈ Z }

Definition 4: ~

A~B if and only if there is a one-to-one correspondence between the elements of A and the elements of B.

Definition 5: Infinitely countable

A set S is said to be infinitely countable if there is a one-to-one correspondence between that set and the set N. That is, S~N.

Theorem 1: The union of two infinitely countable sets is infinitely countable

Proof:

(1) Let A be an infinitely countable set so that A~N

(2) Let B be an infinitely countable set so that B~N

(3) Let O be the set of odd positive integers = {1, 3, 5, ... }

(4) Let E be the set of even positive integers = {2, 4, 6, ... }

(5) N~O since we can map x to 2x-1 such that:

1 --> 1
2 --> 3
3 --> 5
...

(6) N~E since we can x to 2x such that:

1 --> 2
2 --> 4
3 -- > 6
...

(7) O + E = N ~ N

This is true since N consists of all the positive odd integers and all the positive even integers.

(8) A ~ O since A~N and O~N

(9) B ~ E since B~N and E~N

(10) A + B ~ A + B ~ O + E ~ N

QED

Corollary 1.1: The set of integers Z is countable

Proof:

(1) Let W = the set of positive integers = {0, 1, 2, 3, ... }

(2) W ~ N

In this case, x maps to x-1 so that we have:

1 --> 0
2 --> 1
3 --> 2
...

(3) Let Z-= the set of negative integers = {-1, -2, -3, ... }

(4) Z- ~ N

In this case, x maps -x so that we have:

1 --> -1
2 --> -2
3 --> -3
...

(5) Z = Z- + W so Z is countable because it is the union of two countable sets. [Using Theorem 1 above]

QED

Theorem 2: The set of ordered pairs WxW is infinitely countable

The set WxW is infinitely count where W={0, 1, 2, ... } and WxW = { (0,0), (0,1), ..., (1,0), (1,1), ..., (2,0), ... }

Proof:

(1) The trick here is to find a way of ordering WxW so that we can visit each ordered pair one-at-a-time and still be on track to visit all of them.

(2) Here's the ordering:















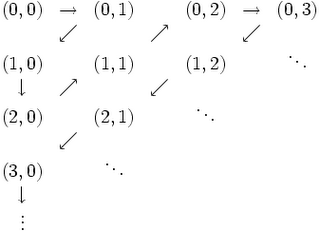
(3) We can see that all possible ordered pairs can be listed in this grid and the zig-zag traversal will eventually visit each one.

QED

Corollary 2.1: If two sets A,B are infinitely countable, then AxB is infinitely countable.

Proof:

(1) Since W ~ N, we can see that A ~W, B~W

(2) This means that AxB ~ WxW

(3) Since WxW ~ N [By Theorem 2 above], we have AxB ~ N.

QED

Theorem 3: All infinite subsets of an infinitely countable set are infinitely countable

Proof:

(1) Let A be an infinite set that is infinitely countable.

(2) Let B be an infinite subset of A.

(3) Now, by definition, we know that we can order the elements in A such that A = {a₁, a₂, ..., a_n }

(4) Now, it follows that B can be listed in the same way with deletions so that you have:

{a_a, a_b, a_c, ... } where a is less than b is less than c etc.

(5) The mapping consists of traversing B in the same order as A so that you have:

1 --> a_a [The first element in A not deleted]
2 --> a_b [The second element in A not deleted]
3 --> a_c [The third element in A not deleted]
...

QED

Theorem 3: The set of rational numbers is infinitely countable

Proof:

(1) The trick here is that we can allow repeats. We come up with an algorithm that will sequentially generate all the rational numbers that exist with repeats.

(2) We can use repeats since by Lemma 2 above, if Q + repeats is infinitely countable then its subset Q (deleting all the repeats) is infinitely countable.

(3) We can map rational numbers to Z x N where Z is the set of integers = { ..., -1, 0, 1, ... } and N is the set of natural numbers = {1,2,3,4, ... } since:

(a) Each rational number q = a/b where a,b ∈ Z. [Definition of rational numbers]

(b) We can assume b is a positive integer since:

b ≠ 0 [Since division by zero is not allowed] and if b ≤ -1, then a/b = (-a)/b where b ≥ 1.

(c) So, every q=a/b maps to (a,b) where a ∈ Z and b ∈ N.

(4) Since Z is infinitely countable (See Corollary 1.1 above) and N is infinitely countable (by definition), we know that ZxN is infinitely countable (By Corollary 2.1 above)

QED

Theorem 4: The number of real numbers between 0 and 1 is not infinitely countable

Proof:

(1) Assume that the real numbers between 0 and 1 is infinitely countable so that there is a mapping between these numbers and N.

(2) Then there should be a complete list. All real numbers would have to be included in this mapping.

(3) But it is possible to construct a number that is not one the list.

(4) All numbers in this list are of the form. 0.xxxxxxxxx....

(5) Let x₁ = the first number in the list and x_1,1 = the first digit of the first number in the list so that 0 ≤ x_1,1 ≤ 9.

(6) Let n₁ = any other digit. For example, if x_1,1 = 9 then we could have n₁ = 8.

(7) We can see that all numbers that we create from n will not equal x₁

(8) Let x_2,2 = the second digit of the second number on the list.

(9) We can now set n₂ = any other digit so that n is now distinct from x₁ and x₂.

(10) We can continue doing this for as long as i and in each case n is different from all the real numbers that came up to i.

(11) In this way, it is possible to set n = a real number which is not on the list.

(12) But this is impossible since we assumed that there was a complete mapping. Therefore, we have a contradiction and we reject our assumption at step #1.

QED

Corollary 4.1: There are an uncountable number of real numbers.

Proof:

This follows directly from the theorem above since (0,1) is a subset of all real numbers so that if (0,1) is uncountable, it follows that the R, the superset of (0,1) is also uncountable.

QED

Corollary 4.2: The number of irrational numbers is uncountable

Proof:

(1) The set of real numbers = the set of rational numbers + the set of irrational numbers.

(2) The set of rational numbers is infinitely countable. [See Theorem 3 above]

(3) Assume that the set of irrational numbers is infinitely countable.

(4) Then the set of real numbers is infinitely countable since it is the union of the rational and the irrational numbers [See Theorem 1 above]

(5) But this contradicts Theorem 4 that the real numbers are not infinitely countable.

(6) Therefore, we have a contradiction and we reject our assumption in step #3.

QED

References

• Countable Set, Wikipedia
• Countability of the Rational Numbers, Cut-The-Knot
  

Heine-Borel Theorem

In today's blog, I present a proof of the Heine-Borel Theorem. This very important theorem is one of the major foundations of topology and calculus. I use this theorem in the proof of the Heine-Cantor Theorem.

Definition 1: open ball B

An open ball of radius ε centered at x₀ is a set of all points in the open interval (x₀ - ε, x₀ + ε).

NOTE: An open interval is an interval that does not include its own endpoints as part of the set.

Definition 2: Upper Bound

A point b is called the upper bound of a set of real numbers A if and only if x ≤ b for all x ∈ A.

Definition 3: Lower Bound

A point c is called the lower bound of a set of real numbers A if and only if c ≤ x for all x ∈ A.

Definition 4: Bounded

A set A is said to be bounded if and only if A has both an upper and lower bound.

Lemma 1: If K is a subset of the real numbers R and K is compact, then K is closed and bounded.

Proof:

(1) Assume that K is a subset of the real numbers and that K is compact. [See Definition 4, here for definition of compact]

(2) Since K is a subset of the real numbers R, then it has the open covering:

K is a subset of ∪ (k=1, ∞) (-k, k) [See Definition 1, here for definition of open covering]

(3) By the definition of compact, each open covering has a finite subcovering so that:

K is a subset of ∪ (k=1, n) (-k, k) [See Definition 3, here for definition of finite subcovering]

(4) But ∪ (k=1,n)(-k,k) is a subset of (-n,n) so k is bounded. [See Definition 4 for definition of bounded]

(5) Assume that K is not closed [See Definition 3, here for definition of closed]

(6) Then, there exists a boundary point x₀ for K which is not in K. [See Definition 1, here for definition of a boundary point, see Lemma 1, here for proof of the existence of x₀ not in K]

(7) For each point x ∈ K, there exists an open ball B_x centered at x and an open ball P_x that is centered at x₀ that do not intersect. [See Definition 1 above for definition of an open ball]

(8) Since there is an open ball B_x for all x ∈ K, ∪ (x ∈ K) B_x is a covering since:

K is a subset of ∪ (x ∈ K) B_x

(9) We have an open covering since the union of open sets is itself open. [See Lemma 3, here]

(10) By the definition of compactness, there must exist a finite subcover such that:

K is a subset of ∪ (k=1, n) B_xk [See Definition 4, here for definition of compact]

(11) We can also define an intersection based on the the n in step #10 and the set of open balls P_x:

Let P₀ = ∩ (k=1,n) P_xk

(12) P₀ is an open set since it is the intersection of a finite set of open sets. [See Lemma 4, here]

(13) But since each ball P_x does not intersect with the ball B_x, it follows that P₀ does not intersect with K [since ∪B_x is a covering of K]

(14) Since x₀ ∈ P₀, it follows that there exists a positive real ε such that (x₀ - ε, x₀ + ε) is a subset of P₀ [This follows from the definition of an open set, see Definition 1, here]

(15) But this is a contradiction since step #14 implies that there exists an ε such that (x0 - ε, x0 + ε) does not include a point from K but from the definition of a boundary point (see Definition 1, here), all such intervals include at least one point of K.

(16) Therefore we must reject our assumption in step #5 and conclude that K is closed.

QED

Definition 5: Neighborhood

Let x be an element of X. A subset N of X is called a neighborhood of x if there is a real number ε greater than 0 such that (x - ε, x + ε) is a subset of N.

Definition 6: Accumulation Point

A point x ∈ X is called an accumulation point of a set S if each neighborhood of x contains infinitely many distinct points of S.

Definition 7: Supremum

The supremum of a bounded set S of numbers is the least upper bound. [See Definition 2 above for definition of upper bound]

Lemma 2: Heine-Borel Lemma

An infinite bounded set possesses at least one accumulation point.

Proof:

(1) Let X be an infinite but bounded set. That is, X contains an infinite number of points. [See Definition 4 above for definition of bounded]

(2) Let a,b be the bounds of X so that X is a subset of [a,b] and a is less than b.

(3) Let m = (a + b)/2

(4) We now can divide up [a,b] into [a,m] and [m,b]

(5) Since [a,b] contains an infinite number of points, either [a,m] or [m,b] must contain an infinite number of points.

(6) Let us select select one of these closed intervals and label its left endpoint a₁ and its right endpoint b₁. So that we have [a₁, b₁] with an infinite number of points.

(7) Let m₁ = (a₁ + b₁)/2.

(8) We can now divide up [a₁,b₁] into [a₁,m₁] and [m₁,b₁]

(9) We can follow the same process as step #6 and define an interval [a₂,b₂] that contains an infinite number of points.

(10) We can repeat this same process to get an a set of intervals [a_i,b_i] where i can be any arbitrary natural number and [a_i,b_i] contains an infinite number of points.

(11) It should also be clear that for each i, a_i ≤ a_i+1 and b_i+1 ≤ b_i. It should also be clear that each a_i ≤ b_i

(12) Putting this together gives us:

a ≤ a₁ ≤ a₂ ≤ ... a_i ≤ b_i ≤ ... b₂ ≤ b₁ ≤ b

(13) So that we have monotonic nondecreasing sequence a_i and a monotonic nonincreasing sequence b_i. [See Definition 8, here for definition of a monotonic sequences]

(14) Let a point c be the supremum for a_i [See definition 7 above for definition of supremum]

(15) Let ε be any positive real number.

(16) It is clear that for each i, b_i+1 - a_i+1 = (1/2)[b_i - a_i]

(17) In fact, b₁ - a₁ = [1/(2¹)][b - a], b₂ - a₂ = [1/(2²)][b - a] and so on so that b_i - a_i = [1/(2ⁱ)][b - a]

(18) Since i can be arbitrarily any number, it follows that there exists a natural number i such that 1/(2ⁱ) ≤ 1/n is less than ε/[b-a] [See Theorem 2, here]

(19) It therefore follows that for there exists a natural number i such that [a_i,b_i] contains an infinite number of points and [a_i,b_i] is a subset of the neighborhood [c - ε, c + ε] since:

1/(2ⁱ) ≤ 1/n is less than ε/[b-a] → 1/(2ⁱ)[b-a] is less than ε

(20) This means that c is an accumulation point. [See definition 6 above for definition of accumulation point]

QED

Lemma 3: The number of open balls with rational radii centered at rationals is countable.

Proof:

(1) The total number of rationals is countable. [See Theorem 3, here]

(2) The set of rational numbers that have open balls centered on them is a subset of all the rationals, so it is also countable.

(3) Since each open ball has rational radii, there is again a countable number of possible radii for each location. [by step #1 again]

(4) This means that the total number open balls with rational radii in on a rational = Q x Q. Since Q is countable, it follows that QxQ is also countable. [See Corollary 2.1, here]

QED

Postulate 1: Axiom of Choice

For any given collection Ω of nonempty subsets of a set X, there exists a function f : Ω → X such that for each S ∈ Ω, we have f(S) ∈ S.

In other words, it is possible to select an item from a list of items. This is one of those postulates that has raised lots of controversy because it is intuitively obvious but surprisingly involves a large number of subtleties. See here for an introduction to the topic.

Lemma 4: Lindelof Principle

Any infinite open cover has a countable subcover

Proof:

(1) Let { O_α } be an open covering for a set K such that each O_α is an open set and K is a subset of ∪ (α) O_α [See Definition 1, here for definition of open covering]

(2) For any point x ∈ O_α, there exists an open interval I_αβ such that it is centered at a rational point and it has a rational radius that lies wholly within O_α [We can do this since there is a rational number between any two real numbers, see Corollary 2.1, here, see Definition 1, here for definition of open set.]

(3) We thus have defined another open covering:

K is a subset of ∪ (α,β) I_αβ

(4) Now, from Lemma 3 above, we know that the number of open balls with rational radii centered at rationals is countable so that we can order the intervals I_αβ to get:

K is a subset of ∪ (n=1,∞) I_n where for each I_αβ there exists an n such that I_αβ = I_n

(5) Now, we can use the Axiom of Choice (see Postulate 1 above), for each I_n, to select an O_α that is a subset of I_n which we can label O_n. In this way, we can obtain the following countable subcover:

K is a subset of ∪(k=1,∞) O_k

QED

Heine-Borel Theorem: The compact sets of the real numbers R are exactly the sets that are both closed and bounded.

Proof:

(1) Using Lemma 1 above, we know that a compact set is closed and bounded. So to establish this theorem, we need to show that a closed and bound subset of the real numbers R is compact.

[See Definition 4, here, for definition of compact; see Definition 4 above for definition of bounded; see Definition 3, here, for closed set.]

(2) Let K be a closed and bounded subset of the real numbers R.

(3) Let { O_α } be an open covering for a set K such that each O_α is an open set and K is a subset of ∪ (α) O_α

(4) Using the Lindelof principle (see Lemma 4 above), we know that we can order { O_α } into an infinitely countable set such that:

K is a subset of ∪ (k=1, ∞) O_k

(5) Assume that no finite subcover for ∪ (k=1, ∞) O_k exists.

(6) Then, so long as we list a finite number of open sets, there must exist at least one point x_n which is an element of K but not an element of this union.

x_n ∉ ∪ (k=1,n) O_k

(7) From this it is possible to construct a set X which consists of an infinite number of distinct points x_n

(a) Let us start with O₁. We know that there is at least one point x₀ ∉ O₁

(b) Now, from step #4, we know that there exists k₁ such that x_n ∈ O_k1. Clearly, there must be a distinct x₁ that is not in the union of O_k and O₁.

(c) We can repeat this process to get as many distinct points as we wish. This means that if X is the set of all these points, X is an infinite set.

(d) Further, we know that each of these x_n elements that make up X have an index based on the ordering in step #4. That is, x₁ is not in O₁, x₂ is not in ∪ {O₁, O₂}, x₃ is not in ∪ {O₁, O₂, O₃ }, etc.

(8) Since K is bounded and X is a subset of K (that is, each x_n ∈ X → x_n ∈ K), it follows that X is also bounded.

(a) Since K is bounded, there exists an upper bound b and a lower bound c such that for all x ∈ K, c ≤ x ≤ b.

(b) Clearly, all x ∈ X are also in K, so b and c are also the upper and lower bound for X.

(9) From the Heine-Borel Lemma above [See Lemma 2 above], we know that there must exist at least one accumulation point c ∈ X.

(10) By the definition of accumulation points (see definition 6 above), every open neighborhood of c contains infinitely many points of X.

(11) Since X is a subset of K, c ∈ K.

(12) So, using step #4, there must be some O_N such that c ∈ O_N.

(13) Since O_N is an open set, then there exists a positive real ε such that:
(c - ε, c + ε) is a subset of O_N.

(14) Since c is an accumulation point, (c - ε, c + ε) contains an infinite number of points in X which means that O_N contains an infinite set of x_n points.

(15) But this contradicts step #6 since:

(a) If O_N contains an infinite number of elements of the form x_n, then it must contain more than N of these elements.

(b) Since each x_n is indexed, this means that at least one element in O_N must be indexed greater than N.

(c) But this is a contradiction since by definition in step #6, O_N cannot contain any x_n with an index such that n is greater than N.

(16) Thus, we reject our assumption in step #5 and conclude that K is compact, that is, for every open covering of K, there is a finite subcovering.

QED

References

• "The Heine-Borel Theorem", Mathematical Physics and Mathematics
• Bert Mendelson, Introduction to Topology, Dover Edition, 1990
• Charles R. MacCluer, Honors Calculus, Princeton University Press, 2006

Compactness

The following content is taken directly from Bert Mendelson's Introduction to Topology. The definitions are used in the proof for the existence of the definite integral (to be added later)

Definition 1: Covering

Let K be a subset of the real numbers R. Let C be a collection of subsets of K. C is a covering of K if and only if the union of all subsets of K in C = K.

An open covering is a covering that is also an open set. [See Definition 1, here for definition of an open set]

Definition 2: Subcovering

S is a subcovering of a set X if S is a subset of C which is a covering of X and S itself is a covering of X.

Definition 3: Finite Subcovering

A subcovering S is a finite subcovering of X if it consists of a finite collection of subsets of X.

Definition 4: Compact

A subset K of the real numbers R is said to be compact if every open covering of K has a finite subcovering.

Theorem: [0,1] is compact

Proof:

(1) Let {O_α}_α∈I be a covering of [0,1] by open sets. [See Definition 1 above for definition of covering, see Definition 1, here for definition of open sets]

(2) Assume that there is no finite subcovering of {O_α}_α∈I [See Definition 3 above for definition of finite subcovering]

(3) This means that at least one of the two closed intervals [0, 1/2] or [1/2, 1] cannot be covered by a finite subcollection of {O_α}_α∈I.

(4) Let [a₁, b₁] denote one of these two intervals of length 1/2 such that it cannot be covered by a finite subcovering.

(5) We may now divide [a₁, b₁ ] into two subintervals of length 1/4:

[ a₁, (a₁ + b₁)/2 ]

and

[(a₁ + b₁)/2, b₁ ]

(6) We know that at least one of these subintervals cannot be covered by a finite subcovering.

(7) Let [ a₂, b₂ ] denote the one of the two subintervals in step #5 that cannot be covered by a finite subcovering.

(8) We can in this way define a sequence of intervals such as:

[a₀, b₀], [a₁, b₁], [a₂, b₂ ], ... , [ a_n, b_n ]

(9) Assume that for i = 0, 1, 2, ..., n we have defined intervals [a_i, b_i] such that:

(a) [a₀, b₀ ] = [0,1]

(b) b_i - a_i = 1/(2ⁱ) for i = 0, 1, ..., n

(c) [a_i+1, b_i+1] = [a_i, (a_i+b_i)/2] or [(a_i+b_i)/2,b_i]

(d) for each i = 0, 1, ..., n, no finite subcovering of {O_α}_α∈I covers [a_i, b_i]

(10) We know that b_i ≥ a_i since b_i - a_i = 1/(2ⁱ) for i = 0, 1, ..., n

(11) We further know that:

a_i ≤ a_i+1 ≤ b_i+1 ≤ b_i

since each time, we the average of (a_i + b_i)/2 ≥ a_i.

(12) From step #11, it follows that for each pair of positive integers m and n, a_m ≤ b_n.

(13) Thus, each b_n is an upper bound of the set { a₀, a₁, a₂, ... }

(14) Let a be the least upper bound of the set { a₀, a₁, a₂, ... }

(15) Then a ≤ b_n for each n and a is the lower bound of the set {b₀, b₁, b₂, ... }

(16) Let b be the greatest lower bound of the set {b₀, b₁, b₂, ... }

(17) We therefore have a ≤ b

(18) By the definition of a and b, we have:

a_n ≤ a ≤ b ≤ b_n for all n.

(19) But this means that b - a ≤ (1/2ⁿ) for all n.

(20) Since n can be any size, (1/2ⁿ) can get arbitrarily small, so that b -a = 0 so that b=a.

(21) a = b ∈ [a,b] [this follows from how we defined a,b]

(22) Since {O_α}_α∈I covers [0,1], it follows that there exists β ∈ I such that a ∈ O_β.

(23) By definition, O_β is an open set, so there exists a positive real number ε such that (a - ε, a + ε) is a subset of O_β [See Definition 1, here for definition of Open Set]

(24) Let us choose a positive integer N that is large enough so that:

1/(2^N) is less than ε

(25) Using step #9, we know then that there exists a_N, b_N such that:

b_N - a_N = 1/(2^N) which is less than ε

(26) Now, a,b ∈ [a_N, b_N] by step #18 so that we have:

a - a_N is less than b_N - a_N = 1/(2^N) which is less than ε

a - b_N = b - b_N is less than b_N - a_N = 1/(2^N) which is less than ε

(27) Consequently, [a_N, b_N] is a subset of (a - ε, a + ε ) which is a subset of O_β

(28) Thus [a_N, b_N] may be covered by a finite subcollection (namely, one!) of {O_α}_α∈I.

(29) This contradicts with step #9d so assumption that no finite subcollection of {O_α}_α∈I can cover the interval [a_n,b_n] so we have a contradiction that emerged from our assumption in step #2.

(30) We therefore reject our assumption in step #2 and conclude that the closed interval [0,1] is compact.

QED

References

• Bert Mendelson, Introduction to Topology, Dover Edition, 1990
  

Boundary Points

In today's blog, I define boundary points and show their relationship to open and closed sets.

Definition 1: Boundary Point

A point x is a boundary point of a set X if for all ε greater than 0, the interval (x - ε, x + ε) contains a point in X and a point in X'.

Lemma 1: A set is open when it contains none of its boundary points and it is closed when it contains all of its boundary points.

Proof:

(1) Let a,b be the boundary points for a set S of real numbers that are not part of S where a is the lower bound and b is the upper bound.

(2) If a,b are not included in S, then we have S = { x : x is greater than a and less than b } which means that x is an open set. [See Lemma 5, here]

(3) If a,b are included in S, then we have S = { x : a ≤ x ≤ b } which means that x is a closed set. [See Lemma 7, here]

QED

Lemma 2: Every real number is a boundary point of the set of rational numbers Q.

Proof:

(1) A boundary point b by definition is a point where for any positive number ε, { b - ε , b + ε } contains both an element in Q and an element in Q'.

(2) So all we need to show that { b - ε, b + ε } contains both a rational number and an irrational number.

(3) We know that this is the case based on the properties of the set of rational numbers and the properties of the set of real numbers.

We can find know that there is at least one rational number in { b - ε, b + ε } [See Corollary 2.1, here]

By the nature of the continuity of real numbers, there exists an irrational number r such that abs(b - r) is less than ε. [See here for a review of the properties of irrational numbers]

QED

References

• Charles R. MacCluer, Honors Calculus, Princeton University Press, 2006
• Bob Gardner, Introductory Level Analysis: Synthesizing R, Rⁿ, Metric Spaces and Topological Spaces.

Open Sets

Today, I talk about open and closed sets. These definitions are needed as part of the foundation of calculus. For example, I will use these properties in my future blog on compactness.

Definition 1: Open Set

A set S that is a subset of the real numbers R is open if and only if for all x ∈ S, there exists ε greater than 0 such that (x + ε, x - ε) is a subset of S.

Lemma 1: ∅ is open

Proof:

This is true since there are no elements of ∅. In other words, for all x ∈ S (none), there exists ε greater than 0 such that (x + ε, x - ε) is a subset of S.

QED

Lemma 2: The set of real numbers R is open

Proof:

(1) Let x be any real number.

(2) Let ε be any real number greater than 0.

(3) (x + ε, x - ε) is a subset of S since for all y ≤ ε, x + y and x - y ∈ R. [By the property of closure, see here for properties of real numbers]

QED

Lemma 3: The union of open sets is open

Proof:

(1) Let { A_i } be a set of open sets.

(2) Let A = ∪ { A_i }

(3) Let x be an element of A.

(4) There must exist an i such that x ∈ A_i

(5) By definition of open sets, there exists ε such that (x + ε, x - ε) is a subset of A_i

(6) But then (x + ε, x - ε) is a subset of A since A_i is a subset of A.

QED

Lemma 4: The intersection of a finite number of open sets is open.

Proof:

(1) Let { A_i } be a finite set of open sets.

(2) Let A ∩ { A_i }

(3) If A = ∅, then A is open, [See Lemma 1 above] so we can assume that A is not ∅.

(4) So there exists x such that x ∈ A

(5) for all i, x ∈ A_i.

(6) Since all A_i are open, for each A_i, there must exist an ε_i greater than 0, such that (x + ε_i, x - ε_i) is a subset of A_i

(7) Let ε = min({ε_i})

(8) Since (x + ε, x - ε) ⊂ (x + ε_i, x - ε_i) for all i, it follows that (x + ε, x - ε) ∈ A = ∩ {A_i}

QED

Lemma 5: (a,b) = { x : a is less than x is less than b } is open

Proof:

(1) Let x be any real number greater than a and less than b.

(2) Let ε = min(abs(a - x),abs(b-x))

(3) So we can see that x + ε ≤ b and a ≤ x - ε.

(4) We can further see that (x + ε/2, x - ε/2) is a subset of (a,b)

QED

Lemma 6: (a, ∞) = { x : a is less than x } is open

Proof:

(1) Let x be any real number greater than a.

(2) Let ε = abs(x - a)/2

(3) It is clear that (x - ε, x + ε) is a subset of (a, ∞)

QED

Definition 2: Complement A'

A' is the complement of A if and only if A' includes all the points that are not in A.

For example if A = negative integers, then A' = nonnegative integers.

Definition 3: Closed Set

A subset of the real numbers R is closed if its complement is open.

Lemma 7: [a,b]= { x : a ≤ x ≤ b } is closed

Proof:

(1) To prove this, we need to show that the complement of [a,b] is open.

(2) So that we have complement[a,b] = { x: x is less than a or x is greater than b }

(3) if x is less than a, then let ε = (a - x)/2. Clearly, { x - ε, x + ε } is a subset of { x : x is less than a or x is greater than b }

(4) if x is greater than b, then let ε = (x - b)/2. Clearly, { x - ε, x + ε } is a subset of { x : x is less than a or x is greater than b }

QED

Lemma 8: [a, ∞ ) = { x : x ≥ a } is closed

Proof:

(1) The complement of this is (-∞, a) = { x : x is less than a }

(2) Since x is less than a, let ε = (a - x)/2.

(3) Clearly, { x - ε, x + ε } is a subset of { x : x is less than a }

QED

References

• Charles R. MacCluer, Honors Calculus, Princeton University Press, 2006
  
• Bob Gardner, Introductory Level Analysis: Synthesizing R, Rⁿ, Metric Spaces and Topological Spaces.
  

Heine-Cantor Theorem

In today's blog, I will talk about uniform continuity and the Heine-Cantor theorem. I use this theorem to establish the definition of the integral.

Definition 1: Uniform Continuity

Given any positive number ε, you can find a value δ such that for all values of u,v in the interval, if absolute(u-v) is less than δ, then absolute(f(u) - f(v)) is less than ε

NOTE: This is different from the definition of continuous at a point (see Definition 1, here for definition of continuous at a point). If a function f is continuous on [a,b], then for any point u in [a,b] and for any arbitrary positive number ε, there exists a value δ greater than 0 such that if v is a number in [a,b] such that abs(u - v) is less than δ, then abs(f(u) - f(v)) is less than ε.

In the case of uniform continuity, we can find a δ which works for all points u. If a function is continuous at a point but not uniformly continuous, then there is at least one δ for a given u that is different than the other δ for the other u's.

Definition 2: Topological Space

A topological space (X,T) is a set X paired with a T which is a set of subsets of X. (X,T) must meet the following conditions;

(a) The empty set ∅ ∈ T

(b) X ∈ T

(c) The intersection of any finite number of sets in T is also in T. If (u_i) is a finite set of elements in T, then ∩u_i ∈ T.

(d) The union of a elements in T is also in T. If (u_i) is a set of elements in T, then ∪ u_i ∈ T.

In the context of a topological space, any subset of X which is an element in T is said to be an open set in relation to this topological space. Any subset of X which is not an element in T is said to be a closed set in relation to this topological space. [See Definition 1, here for definition of open set and Definition 3, here for definition of closed set]

An element of X is said to be a point.

Theorem: Heine-Cantor Theorem

Every continuous function on a compact set is uniformly continuous there

Proof:

(1) Let X,Z be metric spaces. [See Definition 2, here for definition of a metric space]

(2) Let f be a function such that f: X → Z

(3) Let us assume that f is continuous on the compact subset K of X.

(4) Let ε be a real number greater than 0.

(5) Since f is continous on K (see Definition 1, here for Definition of continuous at a point), for each x ∈ K, there exists a real δ(x) greater than 0 such that for y ∈ K:

if d(x,y) is less than δ(x), then d(f(x),f(y)) is less than ε/2.

(6) We see that the set of open balls with center x of radius δ(x)/2 cover K. [See Definition 1, here for a definition of an open ball]

(7) Using the Heine-Borel Theorem (see here), we know that there exists a finite subcovering for K such that:

K = ∪ (i=1,p) B_i where each B_i is centered at x_i.

(8) Let δ be the minimum(δ(x_i/2)) where i is the set of values 1, 2, ..., p.

(9) Let's assume that x,y ∈ K and d(x,y) is less than δ.

(10) Since y ∈ K and since ∪ (i=1,p) B_i is a covering for K, there exists an i such that y ∈ B_i

(11) Since the radius of each ball B_i is δ(x_i)/2, we have: d(y,x_i) is less than δ(x_i)/2.

(12) Since d(x,y) is less than δ and δ is the minimum of all δ(x_i)/2, it follows that:

d(x,y) is less than δ(x_i)/2.

(13) Further, d(x,x_i) less than δ(x_i) since d(x,x_i) ≤ d(x,y) + d(y,x_i) ≤ δ(x_i)/2 + δ(x_i)/2 = δ(x_i) [ d(x,x_i) ≤ d(x,y) + d(y,x_i) is true by the "triangle inequality rule" of metric spaces, see Definition 1, here]

(14) Applying the triangle inequality rule, we have:

d(f(x),f(x₁)) ≤ d(f(x),f(x_i)) + d(f(x_i),f(y))

(15) Since d(x,x_i) is less than δ(x_i), we have d(f(x),f(x_i)) is less than ε/2. [See step #5]

(16) Since d(x_i,y) is less than δ(x_i), we have d(f(x_i),f(y)) is less than ε/2. [See step #5]

(17) Putting #14, #15, and #16 together gives us:

d(f(x),f(x₁)) ≤ d(f(x),f(x_i)) + d(f(x_i),f(y)) is less than ε/2 + ε/2 = ε

(18) Thus, we have shown for every ε greater than 0, there exists a δ such that for all x,y ∈ K,:

d(x,y) is less than δ → d(f(x),f(y)) is less than ε.

QED

References

• Charles R. MacCluer, Honors Calculus, Princeton University Press, 2006
• Topological Space, Wikipedia.Com
• "An Introduction to Metric Spaces", BBC Mathematics Page
  

Introduction to integrals

If derivatives enable us to identify the slope at any point on a continuous function, integrals allow us to calculate the sum of area underneath.

In a previous blogs, I reviewed the foundations of derivatives and some of their advanced properties. In today's blog, I will examine the area under the curve problem and show how definite integrals solve this problem.

The content in today's blog is largely taken from the Wikipedia article on Riemann sums and Edwards and Penney's textbook Calculus and Analytic Geometry.

For purposes of today's blog, I will use the example of the curve f(x) = x³. I will focus on the problem of determining the area under the curve between x=0 and x=2 and y=0. The question at hand is how do we figure out a general method for determining the the total area within these constraints:

One approach to this problem to use a Riemann sum. Reimann sums were first proposed by Bernhard Riemann and today they are a major part of the foundation of calculus.

Now, let me offer a formal definition of a Riemann sum. If you are not interested in formal definitions, feel free to skip this. I will include a more intuitive summary afterwards.

Definition 1: Partition

Let I = [a,b] be a closed interval. [See Definition 3, here for definition of closed interval]

A set P is said to be a partition of I if P is a set of nonempty subintervals = { [a,x₁) [x₁, x₂), ... , [x_n-1,b] } where n, the number of subintervals, is a positive integer and a is less than x₁ which is less than x₂ ... which is less than x_n-1 which is less than b.

Definition 2: Riemann sum

Let f(x) be a real value function on a closed interval I=[a,b] such that f: I → R. Let P be a partition of the interval I.

The Riemann sum S of f over I with respect to a partition P is:

S = ∑ (j=1,n) f(c_j)(x_j - x_j-1)

where c_j is any arbitrary point in [x_j, x_j-1].

If c_j = the minimum in [x_j, x_j-1] for all j, then S is a lower Riemann sum which I will denote as L(P)

If c_j = the maximum in [x_j, x_j-1] for all j, then S is an upper Riemann sum which I will denote as U(P).

The important idea here is that a Riemann sum consists of dividing up a the graph of a function into an arbitrary number of intervals.

Here's a diagram of an upper Riemann sum U(P) where the rectangle corresponds with the maximum point in the interval.


Here is a diagram of a lower Riemann sum L(P) where the rectangle corresponds with the minimum point in the interval.

Now, it should be clear that as we increase the number of subintervals in a partition, both the L(P) and U(P) get closer to the true area under the curve. In fact, we have hit our answer when U(P) = L(P).

The goal of the rest of this blog is to demonstrate that if we continue to increase the number of subintervals, we eventually get to this point. Then, I use Riemann sums to determine the area under the curve where f(x) = x³.

Lemma 1: For any partition P of [a,b], L(P) ≤ R(P) ≤ U(P)

Proof:

(1) Let f(p_j) be the minimum point in each interval [x_j, x_j-1]

(2) Let f(q_j) be the maximum point in each interval [x_j, x_j-1]

(3) It follows that for all j, f(p_j) ≤ f(q_j).

(4) It therefore follows that for all j, f(p_j)(x_j - x_j-1) ≤ f(q_j)(x_j - x_j-1).

(5) And therefore that ∑ (j=1, n)f(p_j)(x_j - x_j-1) ≤ ∑ (j=1,n)f(q_j)(x_j - x_j-1).

(6) It follows that L(P) ≤ R(P) ≤ U(P) since for all j, f(p_j) ≤ f(c_j) ≤ f(q_j).

(7) Applying the same steps as before (step #4 and step #5), we can conclude that:

L(P) ≤ R(P) ≤ U(P)

QED

What makes Riemann sums interesting, is that for any partition P, it is possible refine it. That is, we can increase the number of partitions and get an answer that it closer to the true area under the curve.

Definition 3: Refinement of a Partition

A partition P' is said to be a refinement of a partition P if and only if each subinterval of P' is contained in some subinterval of P.

In other words, each interval in P now corresponds to a unique set of one or more intervals in P' and the total number of intervals in P' is greater or equal to the total number of intervals in P.

Lemma 2: If P' is a refinement of P, then L(P) ≤ L(P') ≤ U(P') ≤ U(P)

Proof:

(1) From Lemma 1 above, we know that:

L(P') ≤ U(P') and L(P) ≤ U(P).

(2) Assume that a partition P' is derived from a partition P by dividing up the kth subinterval [x_k-1, x_k] of P into [x_k-1,z] and [z, x_k] by introducing a point z.

(3) From this perspective, the only difference between L(P) and L(P') is that the term f(p_k)*(x_k - x_k-1) is now replaced by:

f(u)*(z - x_k-1) + f(v)*(x_k - z) where u,v are the minimum points on [x_k-1,z] and [z, x_k] respectively.

If we set L'(P) = L(P) - f(p_k)*(x_k - x_k-1), then we have:

L(P) = L'(P) + f(p_k)*(x_k - x_k-1)

L(P') = L'(P) + f(u)*(z - x_k-1) + f(v)*(x_k - z)

(4) Since f(p_k) is the minimum point for all (x_k-1, x_k), we have:

f(p_k) ≤ f(u)

f(p_k) ≤ f(v)

(5) Hence, it follows that:

f(u)*(z - x_k-1) + f(v)*(x_k - z) ≥ f(p_k)*(z - x_k-1) + f(p_k)*(x_k - z) = f(p_k)*(z - x_k-1 + x_k - z) = f(p_k)*(x_k - x_k-1)

(6) From step #3, we have :

L'(P) + f(u)*(z - x_k-1) + f(v)*(x_k - z) ≥ L'(P) + f(p_k)*(x_k - x_k-1)

So that:

L(P') ≥ L(P)

(7) We can use the same exact reasoning to establish that U(P') ≤ U(P).

(8) So that we have:

L(P) ≤ L(P') [step #6]
L(P') ≤ U(P') [Lemma 1 above]
U(P') ≤ U(P) [Step #7]

QED

Lemma 3: Limit to the lower Riemann sum

Let P_n denote a partition P of the interval [a,b] such that P consists of 2_n subintervals of equal length.

Then, there exists a value I = lim (n → ∞) L(P_n)

Proof:

(1) By Definition 3 above, each P_n+1 is a refinement of P_n.

(2) Using Lemma 2 above:

L(P₁) ≤ L(P₂) ≤ ... ≤ L(P_n) ≤ ...

(3) The sequence { L(P_n) } is a nondecreasing monotonic sequence of real numbers. [See Definition 8, here for a definition of nondecreasing monotonic sequence]

(4) The sequence is clearly bounded since:

(a) Let D = the minimum value of f on [a,b] (See Theorem, here for proof that a minimum exists)

(b) Let U = the maximum value of f on [a,b] (See Lemma 3, here for a proof that the maximum exists)

(c) Since L(P_n) = ∑ (i = 1, 2n) f(p_i)(x_i - x_i-1), it is clear that:

U*(b-a) ≤ L(P_n) ≤ M*(b - a)

(5) Therefore, I must exist since a bounded monotone sequence of real numbers must converge. [See Lemma 1, here]

QED

Definition 4: mesh(P)

The mesh of a partition P is the largest length of x_i - x_i-1.

If all the subintervals that make up the Riemann sum are the same, then mesh(P) = this value. If they are not the same, then mesh(P) = the largest subinterval.

Lemma 4:

For any given real ε greater than 0, there exists a real δ greater than 0 such that if P is a partition of [a,b] with mesh(P) less than δ and P' is a refinement of P, then:

abs(L(P) - U(P)) is less than ε/3 and abs(R(P) - R(P')) is less than ε/3

for any two Riemann sums R(P) associated with P and R(P') associated with P'.

Proof:

(1) Let f be a continous function on the closed interval [a,b]

(2) Since [a,b] is bounded and closed, [a,b] is compact. [See Heine-Borel Theorem, here]

(3) Since [a,b] is compact, f is uniformly continuous on [a,b]. [See Heine-Cantor Theorem, here]

(4) So, there exists a number δ greater than 0 such that if:

abs(u - v) is less than δ, then abs(f(u) - f(v)) is less than ε/[3(b - a)]. [See Definition 1, here for definition of uniformly continuous functions]

(5) Suppose now that P is a partion of [a,b] with mesh(P) less than δ.

(6) Then, abs(U(P) - L(P)) = ∑ (i=1,n) abs(f(q_i) - f(p_i))Δx_i which is less than ε/[3(b-a)]∑(i=1,n) Δx_i = ε/3 [Since ∑(i=1,n) Δx_i= (b - a)].

This is valid since abs(p_i - q_i) is less than δ since mesh(P) is less than δ and p_i and q_i belong to the same interval.

(7) By Lemma 1 above, L(P) ≤ R(P) ≤ U(P) where R(P) = any Riemann sum and this is also true of L(P') ≤ R(P') ≤ U(P') where P' is a refinement of P.

(8) By Lemma 2 above, L(P) ≤ L(P') ≤ U(P') ≤ U(P).

(9) Combining #7 and #8, we can see that R(P) and R(P') are both within the interval [L(P), U(P)] which means that abs(R(P) - R(P')) is less than ε/3 since abs(U(P) - L(P)) is less than ε/3 [From step #6]

QED

This leads us to a definition of a definite integral.

Definition 5: Definite Integral (or Riemann Integral)

∫(a,b) f(x)dx = lim (n → ∞) ∑ (j=1,n) f(c_j)(x_j - x_j-1)

I will try to explain each part of the definition since it is very formal. The ∫ is the notation introduced by Leibniz to indicate the sum of a continuous function (as opposed to ∑ which is the sum of a discrete set of values).

The (a,b) is the closed interval of the integral. The a should really be at the top of the ∫ and the b at the bottom but I am stuck with the limitations of html so this is the notation that I use.

dx is Leibniz's notation for Δx. The idea here is that the integral is the sum of rectangles, that is, an infinitely small width (dx) multiplied with the height f(x) as x varies from a to b.

Putting this together just says the "sum of the continuous function in the closed interval [a,b]".

So, we are defining the integral to mean the limit of the Reimann sum as the partition mesh gets closer and closer to 0.

Lemma 5: abs(a + b) ≤ abs(a) + abs(b)

Proof:

(1) if a,b are both nonegative, then abs(a + b) = a + b = abs(a) + abs(b).

(2) if both are both negative, then abs(a + b) = -(a + b) = -a + -b = abs(a) + abs(b)

(3) if a+b is positive and a is negative, then abs(a + b) = b - a is less than b + (-a) = abs(b) + abs(a) [We can make a parallel argument if a+b is positive and b is negative]

(4) if a+ b is negative and b is positive, then abs(a + b) = -(a + b) = -a -b = abs(a) - abs(b) which is less than abs(a) + abs(b). [We can make a parallel argument if a+b is negative and a is positive]

QED

Corollary 5.1: abs(a + b + ....) ≤ abs(a) + abs(b) + ...

Proof:

(1) We know that abs(a₁ + a₂) ≤ abs(a₁) + abs(a₂) from Lemma 5 above.

(2) Assume that it is true for up to some n so that we have:

abs(a₁ + a₂ + ... + a_n) ≤ abs(a₁) + abs(a₂) + ... + abs(a_n)

(3) Let b = a₁ + a₂ + ... + a_n

(4) abs(b + a_n+1) ≤ abs(b) + abs(a_n+1) [From Lemma 5 above]

(5) Replacing b with a₁ + a₂ + ... + a_n gives us:

abs(a₁ + a₂ + ... + a_n + a_n+1) ≤ abs(a₁) + abs(a₂) + ... + abs(a_n) + abs(a_n+1)

QED

Theorem: For any continuous function, the Riemann sum converges to the area under the curve.

Let I = the area under the curve. Let f be a function continuous on the closed interval [a,b]

For any positive real ε, there exists a positive real δ such that if P is a partition on f in [a,b] such that the mesh(P) is less than δ, then abs(I - R(P)) is less than ε where R(P) = the Riemann sum based on partition P.

Proof:

(1) Let ε be a real greater than 0.

(2) Let δ be a real greater than 0 based on the Lemma 4 above.

(3) By Lemma 3 above, there exists a δ₂ such that there if we find an n such that mesh(P_n) is less than min(δ,δ₂), then abs(L(P_n) - I) ≤ ε/3.

(4) Let P = P_n and let P' be a refinement on P.

(5) Then, abs(R(P) - R(P')) ≤ ε/3. [From Lemma 4 above]

(6) Further, since R(P') is in between L(P') and U(P') [from Lemma 1 above] and L(P) ≤ L(P') ≤ U(P') ≤ U(P) [from Lemma 2 above], it follows that:

abs(L(P) - R(P')) ≤ abs(L(P) - U(P)) ≤ ε/3 [From Lemma 4 above]

(7) abs(I - R(P)) = abs(I - L(P) + L(P) - R(P') + R(P') - R(P))

(8) Using Corollary 5.1 above, we have:

abs(I - L(P) + L(P) - R(P') + R(P') - R(P)) ≤ abs(I - L(P)) + abs(L(P) - R(P')) + abs(R(P') - R(P))

(9) Since abs(I - L(P)) is less than ε/3 [step #3 since P = P_n] and abs(L(P) - R(P')) is less than ε/3 [step #6] and abs(R(P') - R(P)) is less than ε/3 [step #5], we have:

abs(I - R(P)) is less than abs(I - L(P)) + abs(L(P) - R(P')) + abs(R(P') - R(P)) which is less than ε/3 + ε/3 + ε/3 = ε

QED

Example: Using a Riemann sum to estimate the area under f(x) = x³ on the closed interval [0,b]

(1) Using the definition of a Riemann sum, we can now use the Theorem above to get:

∫(0,b) f(x)dx = lim (n → ∞) ∑ (i=1,n) f(c_i)Δx

(2) If we divide up P into n equal subintervals, then we can set Δx = b/n and set c_i = ib/n. This then gives us:

∫(0,b) x³dx=lim (n → ∞) ∑ (i=1,n) (ib/n)³(b/n) = lim (n → ∞) ∑(i=1,n)(i³b⁴/n⁴)

(3) Since b,n are constants, we have:

lim (n → ∞) (i³b⁴/n⁴) = lim (n → ∞) (b⁴/n⁴) ∑(i=1,n)(i³)

(4) Using Lemma 4, here,

lim (n → ∞) (b⁴/n⁴) ∑(i=1,n)(i³) =lim (n → ∞) (b⁴/n⁴)[(1/4)n⁴ + (1/2)n³ + (1/4)n²]=

= lim (n → ∞) (b⁴)[(1/4) + (1/2)/n + (1/4)/n²]

(5) Since n is approaching ∞, this means that:

(1/2)/n and (1/4)/n² approach 0 giving us:

lim (n → ∞) (b⁴)[(1/4) + (1/2)/n + (1/4)/n²] = b⁴/4.

This example shows the limitation of using Riemann sums to determine the integral. It makes a lot of sense as an explanation of how the integral relates to a limit. It presents problems when it comes down to applying it to a more general set of equations. If a summation formula exists, then the Riemann sum works fine. If a summation formula does not exist, then the Riemann sum, by itself, does not get us to a final result.

A much more powerful method for determining integrals is to view them as antiderivatives. That is, take the inverse of the derivative and the answer is the integral. How do we know that this works? This very important result is called the Fundamental Theorem of Calculus and I will go over its proof in my next blog.

References

• Riemann Sum, Wikipedia
• Riemann Sum, PlanetMath.org
• Edwards & Penney, Calculus and Analytic Geometry