This represents a very basic introduction that is meant to provide background for my larger blog on Fermat's Last Theorem: n = 5 (see here).
Today's blog is based on the work by Harold M. Stark in his book An Introduction to Number Theory.
1. Matrix defined
A matrix is a grouping of numbers that allows working on all the numbers at the same time.
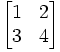
For example, let's consider a 2 x 2 matrix that can be based on a set of numbers: 1, 2, 3, 4.
The matrix itself looks like this:
2. Addition and subtraction of matrices
Addition and subtraction of matrices are exactly the same as if you added and subtracted the numbers independently:
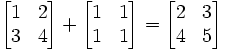
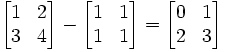
3. Multiplication of Numbers with Matrices
Multiplication with an integer just applies the integer to all the values involved so that:
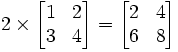
4. Product of Two Matrices
In addition to these properites, matrices have there own special operations. The product of 2 matrices is a bit confusing. We define a product of a 1 x 2 matrix with a 2 x 2 matrix as the following:
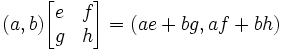
We define a product a 2 x 2 matrix with a 2 x 2 matrix as the following:
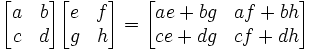
Now, here's where it gets a bit confusing. We normally refer to a matrix using a capital letter. So let's say we have two matrices A,B such that: A is a 2x2 matrix and B is a 2x2 matrix. We cannot assume that AB = BA. For example, if we reverse the matrices above, we get the following equation:
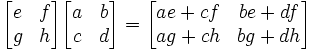
Another important point is that there is no product defined for a 2x1 matrix and a 2x2 matrix or a 2x2 matrix and 1x2 matrix (since order is important in matrix products) and for that matter, there is no product defined a 2x2 matrix with a 1x2 matrix. In the case of 2x2 matrices, you can only get a product for a 2x2 matrix with a 2x2 matrix or a 1x2 matrix with a 2x2 matrix.
5. Determinant
A determinant is a value that is derived from a 2x2 matrix. Here is the definition:
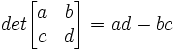
Lemma 1: det(AB) = (detA)(detB)
(1) Let A =
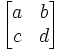
Let B =
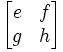
(2) AB =
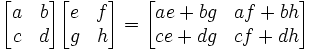
(3) det(AB) = (ae+bg)(cf+dh) - (af+bh)(ce+dg) = (acef + adeh + bcfg + bdgh) - (acef + adfg + bceh + bdgh) = adeh + bcfg - adfg - bceh.
(4) det(A) = ad - bc
(5) det(B) = eh - fg
(6) So det(A)det(B) = (ad - bc)(eh - fg) = adeh + bcfg - adfg - bceh
QED
6. Identity Matrix
The Identity Matrix is referred to as I and defined as:
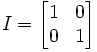
Lemma 2: AI = IA = A
(1) Let A =
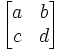
(2) AI =
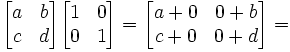
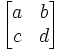
(3) IA =
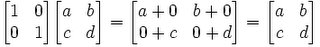
QED
7. Inverse
Let A =
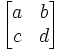
We denote the inverse of A as A-1 and we define it as:
A-1 =
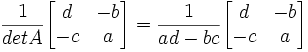
Lemma 2: AA-1 = A-1A = I
(1)
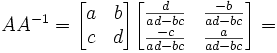
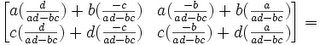
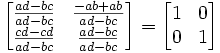
(2)
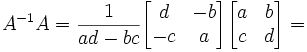
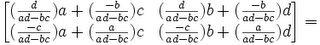
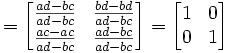
QED
Lemma 3: det A-1 = 1/(det A)
(1) (det A)(det A-1) = det(AA-1) [From Lemma 1]
(2) det(AA-1) = det(I) [From Lemma 2]
(3) det(I) = 1*1 - 0*0 = 1. [Definition of I, Definition of Determinant]
(4) So, (det A)(det A-1) = 1
(5) And dividing both sides by (det A) gives us:
det A-1 = 1/(det A)
QED
7. Final Points
The last point here is that while AA-1 = I, it is not necessarily true that ABA-1 = B. The reason is that AB does not necessarily equal BA and we are not allowed to change the order of the matrix elements.