Review of Matrices

In today's blog, I will review some very basic results in 2x2 and 1x2 matrices.

This represents a very basic introduction that is meant to provide background for my larger blog on Fermat's Last Theorem: n = 5 (see here).

Today's blog is based on the work by Harold M. Stark in his book An Introduction to Number Theory.

1. Matrix defined

A matrix is a grouping of numbers that allows working on all the numbers at the same time.

For example, let's consider a 2 x 2 matrix that can be based on a set of numbers: 1, 2, 3, 4.

The matrix itself looks like this:


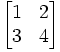
2. Addition and subtraction of matrices

Addition and subtraction of matrices are exactly the same as if you added and subtracted the numbers independently:




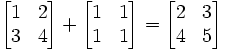
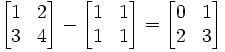
3. Multiplication of Numbers with Matrices

Multiplication with an integer just applies the integer to all the values involved so that:


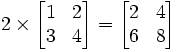
4. Product of Two Matrices

In addition to these properites, matrices have there own special operations. The product of 2 matrices is a bit confusing. We define a product of a 1 x 2 matrix with a 2 x 2 matrix as the following:


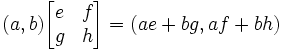
We define a product a 2 x 2 matrix with a 2 x 2 matrix as the following:


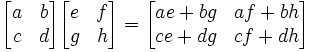
Now, here's where it gets a bit confusing. We normally refer to a matrix using a capital letter. So let's say we have two matrices A,B such that: A is a 2x2 matrix and B is a 2x2 matrix. We cannot assume that AB = BA. For example, if we reverse the matrices above, we get the following equation:


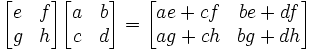
Another important point is that there is no product defined for a 2x1 matrix and a 2x2 matrix or a 2x2 matrix and 1x2 matrix (since order is important in matrix products) and for that matter, there is no product defined a 2x2 matrix with a 1x2 matrix. In the case of 2x2 matrices, you can only get a product for a 2x2 matrix with a 2x2 matrix or a 1x2 matrix with a 2x2 matrix.

5. Determinant

A determinant is a value that is derived from a 2x2 matrix. Here is the definition:


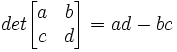
Lemma 1: det(AB) = (detA)(detB)

(1) Let A =


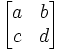
Let B =


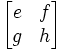
(2) AB =


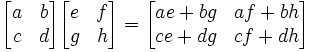
(3) det(AB) = (ae+bg)(cf+dh) - (af+bh)(ce+dg) = (acef + adeh + bcfg + bdgh) - (acef + adfg + bceh + bdgh) = adeh + bcfg - adfg - bceh.

(4) det(A) = ad - bc
(5) det(B) = eh - fg
(6) So det(A)det(B) = (ad - bc)(eh - fg) = adeh + bcfg - adfg - bceh

QED

6. Identity Matrix

The Identity Matrix is referred to as I and defined as:


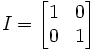
Lemma 2: AI = IA = A

(1) Let A =


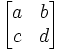
(2) AI =


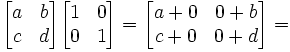
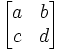
(3) IA =


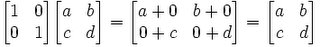
QED

7. Inverse

Let A =


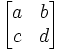
We denote the inverse of A as A^-1 and we define it as:
A^-1 =



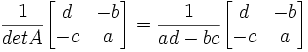
Lemma 2: AA^-1 = A^-1A = I

(1)






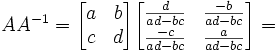
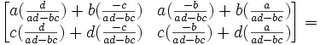
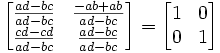
(2)




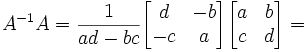
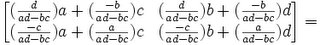
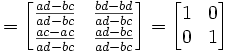
QED

Lemma 3: det A^-1 = 1/(det A)

(1) (det A)(det A^-1) = det(AA^-1) [From Lemma 1]

(2) det(AA^-1) = det(I) [From Lemma 2]

(3) det(I) = 1*1 - 0*0 = 1. [Definition of I, Definition of Determinant]

(4) So, (det A)(det A^-1) = 1

(5) And dividing both sides by (det A) gives us:
det A^-1 = 1/(det A)

QED

7. Final Points

The last point here is that while AA^-1 = I, it is not necessarily true that ABA^-1 = B. The reason is that AB does not necessarily equal BA and we are not allowed to change the order of the matrix elements.