Generalized Power Rule

In today's blog, I continue review of the basics of calculus and derivatives. Today, I will go over the Generalized Power Rule for Derivatives.

This rule can be used in the the proof for Taylor's Formula.

Lemma 1: The Root Rule

dy/dx(x^(1/q)) = (1/q)x^(1/q)-1

Proof:

(1) Let y = x^(1/q)

(2) Then, x = y^q

(3) dx/dy(y^q) = qy^q-1 [From the Power Rule, see here]

(4) dy/dx = 1/(dx/dy) = 1/(qy^q-1)

(5) Applying (#1) to (#4) gives us:

dy/dx = 1/(q[x^(1/q))^q-1]) =
= (1/q)(1/[x^{1 - (1/q)}]) =
= (1/q)(x^(1/q)-1)

QED

Lemma 2: The Chain Rule

If a function f is differentiable at x and a function g is also differentiable at f(x), then if h is a function such that h(x) = g(f(x)), then h'(x) = g'(f(x))*f'(x)

Proof:

(1) Let x₀ be a point where f is differentiable.

(2) Let y₀=f(x₀) and be a point where g is differentiable.

(3) Let k(Δx) = f(x₀ + Δx) - f(x₀) where Δx is nonzero and k(Δx) is nonzero.

(4) Then:

[g(f(x₀ + Δx)) - g(f(x₀))]/Δx =

= [[g(f(x₀) + k(Δx)) - g(f(x₀))]/k(Δx)]*[(k(Δx)/Δx]

(5) Let's define a function φ such that:


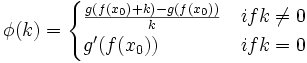
(6) We can see that φ is continuous at k=0 since differentiability implies continuity (see Lemma 4 here)

(7) So, from (3), we see that:
lim (k → 0) φ(k) = g'(f(x₀)).

(8) Now, lim(Δx → 0) k(Δx) = lim(Δx → 0)[f(x₀ + Δx) -f(x₀)] = f(x₀)-f(x₀) = 0

(9) Because f is continuous at x₀ and because φ(0) = g'(f(x₀)), we conclude from (#5):

lim (Δx → 0) φ(k(Δx)) = g'(f(x₀))

(10) Applying #5 to #4 gives us
[[g(f(x₀) + k(Δx)) - g(f(x₀))] /k(Δx)]*[k(Δx)/Δx] = φ(k(Δx))*[k(Δx)/Δx]

(11) Applying #3 to #10 gives us
φ(k(Δx))*[k(Δx)/Δx] = φ(k(Δx))*[[f(x₀ + Δx) - f(x₀)]/(Δ x)]

(12) Using #4 thru #11 gives us:

lim (Δx → 0) [g(f(x₀ + Δx)) - g(f(x₀))]/Δ x =

= lim (Δ x → 0) φ(k(Δx))*[f(x₀ + Δx) - f(x₀)]/Δ x =

= g'(f(x₀))*f'(x₀)

QED

Corollary: if n is an integer, then D[f(x)]ⁿ = n[f(x)]^n-1f'(x)

(1) Let g(u) = uⁿ where n is an integer

(2) g'(u) = nu^n-1 [By the Power Rule for Derivatives, see here]

(3) Now, if u = f(x), then g'(u) = g'(f(x))*f'(x) [From Chain Rule above]

(4) So, D[f(x)]ⁿ/dx = n[f(x)]^n-1*f'(x) [From #2 and #3]

QED

Theorem: Generalized Power Rule

If x is differentiable at x and r is a rational number, then:
D([f(x)^r])/dx = r[f(x)]^r-1*f'(x)

Proof:

(1) [f(x)]^(p/q)] = {[f(x)]^p}^(1/q) = u^(1/q) where p,q are positive integers and u = [f(x)]^p

(2) Du/dx = p[f(x)]^p-1f'(x) [From the Corollary above]

(3) D[f(x)]^(p/q)/dx = Du^(1/q)/dx =

= (1/q)u^(1/q)-1Du/dx [From the Root Rule above]

= (1/q){[f(x)]^p}^(1/q)-1p[f(x)]^p-1f'(x) [From step # 2 above]

= (p/q)[f(x)]^{p((1/q)-1)+p-1}f'(x)

= (p/q)[f(x)]^(p/q)-1f'(x)

QED

References

• Edwards & Penny, Calculus and Analytic Geometry