Introduction to Matrices

A matrix is a rectangular array of elements; it can be composed from any set of elements arranged evenly into rows and columns. While these elements can themselves be matrices, for purposes of this blog, I will assume that the elements are numbers.

Definitition 1: Matrix

A matrix is an ordering of elements into rows and columns. A matrix M that is an r x c matrix consists of r rows and c columns.

For example, a 2 x 3 matrix contains 6 elements ordered into 2 rows and 3 columns.

I will refer to a matrix as a capital letter and the elements that make up a matrix as a lowercase letter followed by a subscript that specifies row and column.

For example, a 2 x 3 matrix M consists of the following elements: m_1,1, m_1,2, m_1,3, m_2,1, m_2,2, m_2,3 that would look like this:



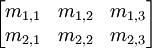
So that we have, M = [ m_i,j ]_{2 x 3}

Definition 2: Matrix Equality

If A is an m x n matrix and B is a p x q matrix, then A = B if and only if m=p and n=q and a_i,j = b_i,j for all i in (1 .. m) and for all j in (1 .. n).

In other words, two matrices are equal if they consist of the same number of rows and columns and all their elements are equal.

Definition 3: Matrix Addition

If A, B are two matrices of the same dimensions m x n, then the sum C = A + B is given by:

c_i,j = a_i,j + b_i,j for all i in (1 .. m) and all j in (1 .. n)

where C is also an m x n matrix.

For example:



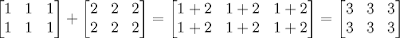
Matrices can be only be added together when they consist of the same number of rows and columns.

Definition 4: Scalar

A scalar is any element of a matrix which is a number.

In this blog, I have made the assumption that all the elements of a matrix are scalar.

I will represent a scalar value as a lowercase letter that does not have a subscript.

Definition 5: Scalar Multiplication

If a is a scalar and B is an m x n matrix, then C = aB is also an m x n matrix such that:

c_i,j = a*b_i,j for all i in (1..m) and for all j in (1 .. n).

For example:



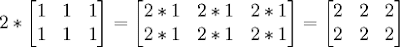
In my next blog, I will review matrix multiplication.

References

• Hans Schneider, George Philip Barker, Matrices and Linear Algebra, 1989.