Let P1, P2 ∈ F[X].
We say that P2 divides P1 if there exists Q ∈ F[X] such that P1 = P2Q
Definition 2: GCD for Polynomials
A greatest common divisor (GCD) of P1, P2 is a polynomial D ∈ F[X] which has the following properties:
(a) D divides P1 and P2
(b) If S is a polynomial which divides P1 and P2, then S divides D.
Definition 3: Relatively prime polynomials
Two polynomials P1, P2, then P1, P2 are said to relatively prime polynomials if the only factors they have in common are of degree 0.
Definition 4: degree: deg
The deg of a polynomial P is the greatest integer n for which the coefficient Xn in the expression of P is not zero.
Theorem 1: Euclid's Algorithm for Greatest Common Divisor for Polynomials
For any two polynomials P1, P2, there exists a GCD
Proof:
(1) Let P1, P2 be any two polynomials such that deg P1 ≥ deg P2
(2) If P2 = 0, then P1 is the GCD of P1, P2 [See Definition 2 above]
(3) Otherwise, we divide P1 by P2 using the Euclidean Division Algorithm for Polynomials. [See Theorem, here]
(4) Then there exists two polynomials Q1, R1 such that:
P1 = Q1P2 + R1
and deg R1 is less than deg P2.
(5) If R1 = 0, then P2 is the GCD of P1, P2
(6) Next, we divide P2 by R1 to get:
P2 = Q2R1 + R2
and deg R2 is less than deg R1
(7) If R2 ≠ 0, then we can set up the following equations:
(a) R1 = Q3R2 + R3
(b) R2 = Q4R3 + R4
...
(c) Rn-2 = QnRn-1 + Rn
(d) Rn-1 = Qn+1Rn + Rn+1
(8) Since deg P2 is greater than deg R1 which is greater than deg R2 which is greater than ... deg Rn which is greater deg Rn+1, this sequence cannot extend indefinitely.
(9) Therefore, Rn+1 = 0 for some n.
(10) Rn divides P1, P2 since:
Because Rn+1=0, Rn divides Rn-1
Because Rn divides Rn-1, from equation 7c, Rn divides Rn+1
We can now proceed up each of these implied equations in the same way until we get to 7b.
Since we have shown that Rn divides R2 and R3 before it, it is clear from 7a, that Rn divides R1
It is clear from step #6 that Rn divides P2 and clear from step #4 that Rn divides P1
(11) Assume that P1 and P2 are both divisible by a polynomial S.
(12) Then by step #4, S must divide R1.
(13) By step #6, S must divide R2
(14) We can now use the same argument to go through the equations in step #7 to conclude that S must likewise divide Rn.
(15) This proves that Rn is the GCD for P1,P2 [See Definition 2 above]
QED
Definition 5: monic polynomial
A polynomial is monic if and only if its leading coefficient is 1.
Theorem 2:
Any two polynomials P1, P2 ∈ F[X] which are not both 0 have a unique monic greatest common divisor D1 and a polynomial D ∈ F[X] is a greatest common divisor of P1, P2 if and only if D=cD1 for some c ∈ Fx (= F - {0}).
Proof:
(1) Let P1 ∈ F[X] be polynomials such that deg P1 is greater than deg P2
(2) Using Theorem 1 above, we know that there exists Rn such that Rn is the GCD of P1, P2
(3) Dividing Rn by its leading coefficient gives us a monic GCD of P1,P2
(4) Assume that D, D' are GCD's of P1, P2
(5) Then D divides D' and D' divides D. [See Definition 2 above]
(6) Then there exists polynomials Q,Q' ∈ F[X] such that:
D' = DQ
D = D'Q'
(7) So that:
Q = D'/D
Q' = D/D'
QQ' = (D'/D)(D/D') = 1
(8) But since Q'Q=1, they must both be constants which are inverses of each other.
(9) So, if D and D' are monic, then Q=Q'=1 and D=D' [Otherwise if Q ≠ 1, then D'=DQ would imply that D' is not be monic]
(10) Suppose D is any GCD of P1, P2
(11) Let D' be the unique monic GCD of P1, P2
(12) Let a = the leading coefficient of D.
(13) It is clear that (1/a)D = D' since the monic GCD is unique [see Step #9 above]
QED
Theorem 3:
If D is the GCD of P1, P2, then there exists polynomials U1, U2 such that:
D = P1U1 + P2U2 where U1, U2 ∈ F[X]
Proof #1:
(1) Using step #7c from Theorem 1 above, we have:
Rn-2 = QnRn-1 + Rn
which gives us:
Rn = Rn-2 - QnRn-1
and likewise:
Rn-1 = Rn-3 - Qn-1Rn-2
(2) We can then use the same type of equation to resolve Rn-1 to get:
Rn = Rn-2 - Qn(Rn-3 - Qn-1Rn-2) =
= Rn-2 - QnRn-3 + QnQn-1Rn-2 =
= -Rn-3Qn + Rn-2(1 +QnQn-1)
(3) We've now put Rn in terms of Rn-3 and Rn-2
(4) In this way, we can eliminate each Ri in terms of Ri-1 and Ri-2 up until we resolve R1 into P1, P2
(5) Eventually we get to an expression of Rn such that:
Rn = P1U1 + P2U2
QED
Proof #2:
(1) From step #4 of Theorem 1 above, we have:
P1 = Q1P2 + R1
(2) Using Matrix Theory (see here for review of 2 x 2 matrices), this gives us:

(3) From step #6 of Theorem 1 above we have:
P2 = Q2R1 + R2
which gives us:

(4) We can continue this approach until step #7d:
Rn-1 = Qn+1Rn + Rn+1
which gives us:

(5) Combining the matrix equations gives us:

(6) Now, since we know that:


(7) We see that each:

is invertible (see here for review of invertibility of matrices).
(8) We can then rearrange the equation in step #5 to be:
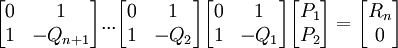
(9) Now, we can define U1, U2, U3, U4 such that:

(10) It now follows that:

(11) This then gives us that:
U1*P1 + U2*P2 = Rn
and
U3*P1 + U4*P2 = 0
QED
Corollary 3.1:
If P1, P2 are relatively prime polynomials in F[X], then there exists polynomials U1, U2 such that:
P1U1 + P2U2 = 1
Proof:
Since for relatively prime polynomials GCD = 1, this result follows directly from Theorem 3 above.
QED
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001
No comments :
Post a Comment