It turns out that the Pythagorean Theorem is itself a proof for the existence of irrational numbers. For example, if a=1, b = 1, then c = √2. Here in lies one of the most famous irrational numbers.
Theorem: if p is a prime then √p is irrational.
(1) Assume that there exists two values a,b such that: a/b = √p and such that a,b are the lowest positive fraction such that gcd(a,b)=1.
NOTE: We know that in fractions, if a,b had any common factors, then we could divide them off and still maintain the same ratio.
(2) Then a2/b2 = p and therefore a2 = pb2.
(3) So, we see that p divides a. So there exists a value a' such that a=pa'. [This is true by Euclid's Lemma since p is a prime and it divides either a or a]
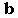
(4) So, we get (pa')2 = pb2 which means that p2a'2 = pb2.
(5) Dividing both sides by p, we get: pa'2 = b2.
(6) But now we see that p divides b (again by Euclid's Lemma). This is a contradiction since a,b do not have any common divisors so we can reject our initial assumption.
QED
Lemma 1: if α is irrational, a,b are rational, and b ≠ 0, then a + bα is irrational
(1) Let x = a + bα
(2) bα = x - a
(3) α = (x - a)/b
(4) Now, this proves that x is not rational. Since if x is rational, then (x-a)/b would be rational, but this is impossible since (x-a)/b = α which is irrational.
QED
Lemma 2: if α is irrational, then 1/α is irrational
(1) Let y = 1/α
(2) Then, α = 1/y.
(3) This proves that y is not rational. If it were, then 1/y would be rational but it isn't since 1/y = α which is irrational.
QED
Lemma 3: if a,b are rational and α is irrational, and a + bα is rational, then a=b=0.
(1) By Lemma 1 above, if a + bα is rational, then b = 0.
(2) Since a + bα = 0 we know that a = 0 - bα = 0 - 0 = 0
QED
Lemma 4: For any positive real number ε, there exists a positive irrational number that is less than ε
Proof:
(1) Let p be a prime such that √p is greater than 1/ε [We can make this assumption based on Euclid's Theorem about infinite primes, see here]
(2) By the Theorem above, we know that √p is an irrational number.
(3) Now, if based on step #1, we know that:
1/√p is less than ε
(4) We also know that 1/√p is an irrational number from Lemma 2 above.
QED
Corollary 4.1: For any two distinct rational numbers, there exists an irrational number that is in between.
Proof:
(1) Let x,y be two distinct rational numbers where x is greater than y.
(2) We can see that if ε is any positive number less than x - y, then, y + ε lies in between x and y.
(3) By Lemma 4 above, we know that there exists an irrational number α that is less than ε.
(4) Further, we know that y + α is also irrational [by Lemma 1 above] and we know that y + α lies in between x and y.
QED
10 comments :
Lemma 1: if α is irrational and b ≠ 0, then a + bα is irrational.
In its current form this lemma is incorrect.
It should be:
Lemma 1: if α is irrational, a is rational and b ≠ 0, then a + bα is irrational
Thanks for the comment. I agree with your suggestion about making the lemma clearer -- I've updated the blog entry.
Cheers,
-Larry
In Lemma 1, doesn't b have to be rational as well?
Rob
Hi Rob,
I've updated the blog to make it clearer that b must also be rational.
Cheers,
-Larry
This in response to Corollary 4.1.
What if x and y are any numbers (i.e. the could be either irrational or rational)?
Hi Yo_Shi,
You are right. There is always an irrational number between any two real numbers.
-Larry
Is corollary 4 indeed rigorous?
We have established that x < y+ε < y, and that we can find an irrational number α such that α < ε. Hence we can say that x < y+α, where y+α is irrational. But we cannot assert that y+α < y. It may, for all we know, that x < y < y+α.
In fact, based on the crude way that we pick our irrational number (i.e. the reciprocal of the square root of a rational number), we can let x = 1, y = 9/10, and find that there is in fact no such α that lies in the open interval (x, y).
Hi Anonymous,
To be clear, we are assuming that x > y so that y < y + ε < x.
If ε is a positive number less than x-y (which is positive), it follows that:
y + ε > y (since ε is positive)
x > y + ε (since ε is less than x - y)
-Larry
Lemma 3:
should
if a,b are rational and α is irrational, and a+bα is rational, then a=b=0.
be
if a,b are rational and α is irrational, and a+bα=0, then a=b=0.
In Corollary 4.1
ε is any positive number less than x-y.
How do you prove the existence of ε?
You need a Lemma saying that for any positive number there is a smaller positive number.
You can use Lemma 4 to get an irrational number ε that is less than x-y.
But then there is no need to use Lemma 4 again to get an α that is less than ε..
x+ε would then be a sufficient irrational number between x and y.
Rob
Post a Comment