limit (θ → 0) sin θ/θ = 1

Today's proof is part of the review of basic properties that I use to determine the derivatives of sine x and cosine x. This is part of the larger story where I show how the Taylor Series can be used to define sin and cosine independently of Euclid.

To be clear, I am using Euclidean Geometry to determine the derivative for sin x and cosine x, then I am using the Taylor Series to show that these results are equivalent to an infinite series that makes no such assumption. These ideas form the foundation of Euler's Identity which is one of the most amazing results in all of mathematics.

Lemma 1: if (a/b) is greater than (c/d), then d/c is greater than b/a

Proof:

(1) Let n be a positive value such that 10ⁿ that is greater than (a/b).

(2) 10ⁿ / (c/d) is greater than 10ⁿ/(a/b) since any number can be divided more times by a smaller amount.

(3) But now, if we divide both sides of the equation by 10ⁿ, we get:

1/(c/d) is greater than 1/(a/b)

which means that:

d/c is greater than b/a

QED

Lemma 2: lim(θ → 0) sin θ/θ = 1



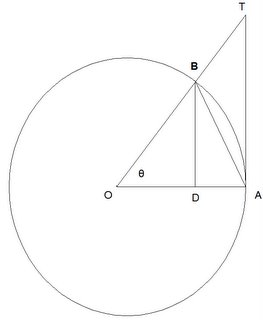
Proof:

(1) Let r be the length of the radius of circle O.

(2) The area for triangle OAB = (1/2)r*(r*sin θ) [See here for details if needed]

= (1/2)r²*sin(θ)

(3) The area of the sector OAB = (1/2)r²θ [Proof to be added later]

(4) The area of the triangle OAT = (1/2)r²tan(θ)

[Since the area of a triangle is (1/2)base*height, see here if needed, with base = r and height = r*tan(θ), see here if needed]

Now, since tan(θ) = sin(θ)/cos(θ) [see here if needed], then we have:

The area of triangle OAT = (1/2)r²(sin θ)/(cos θ)

(5) So, we can see that:

area of triangle OAB is less than area of the sector OAB which is less than area of the triangle OAT.

So that:

(1/2)r²(sin θ) is less than (1/2)r²θ which is less than (1/2)r²(sin θ)/(cos θ)

(6) Dividing all sides by (1/2)r² gives us:

sin θ is less than θ which is less than sin(θ)/cos(θ)

(7) Now, if we divide (5) by sin θ (assuming sin θ ≠ 0), then we get:

1 is less than θ/(sin θ) which is less than 1/cos(θ)

Taking the reciprocal for each value gives us:

1 is greater than (sin θ/θ) which is greater than cos(θ).

(8) Now, we know that the limit (θ → 0) 1 = 1, by the Constant Law (see here).

(9) We know that lim(θ → 0) cos(θ) = 1 since:

(a) cos θ is a continuous function (see here if more details are needed)

(b) so this means lim (θ → 0) cos θ = cos 0 = 1 (see here for definition of continuous functions, see here for review of why cos 0 = 1)

(10) But now, we can apply the Squeeze Rule (see here), to get:

lim (θ → 0) (sin θ/θ) = 1.

QED