sin x < x < tan x for x in (0,π/2)

In today's blog, I will show how it is possible to use a unit circle to establish that if x is greater than 0 and less than π/2, then sin x is less than x which is less than tan x.

Theorem: if x is in (0,π/2), then sin x is less than x is less than tan x



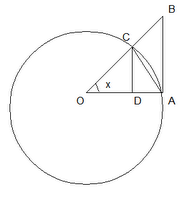
Proof:

(1) Let O be a circle with radius = 1.

(2) Let ∠ CDO and ∠ BAO be right angles.

(3) Let x be the angle at ∠ COD

(4) We can see the following values apply to this diagram

cos x = adjacent/hypotenuse = OD/OC = OD/1 = OD

sin x = opposite/hypotenuse = CD/OC = CD/1 = CD

tan x = sin x/cos x = opposite/adjacent = AB/OA =AB/1 = AB

(5) Area of triangle OAC = (1/2)(base)(height) = (1/2)(OA)(CD) = (1/2)(1)(sin x) = (1/2)(sin x) [See Lemma 2, here for proof]

(6) Area of sector OAC = (1/2)(x)(radius)² = (1/2)(x)(1)² = (1/2)x [See Lemma 2, here for proof]

(7) Area of triangle OAB = (1/2)(base)(height) = (1/2)(OA)(AB) = (1/2)(1)(tan x) = (1/2)(tan x) [See Lemma 2, here for proof]

(8) By the diagram above, it is clear that triangle OAB is greater than sector OAC which is greater than triangle OAC.

(9) This then gives us that (1/2)(tan x) is greater than (1/2)(x) which is greater than (1/2)(sin x).

(10) Dividing all values by (1/2) gives us:

tan x is greater than x which is greater than sin x.

QED

References

• Use of Squeezing Theorem to Find Limits, analyzemath.com