The set of natural numbers N = { 1, 2, 3, ... }
Definition 2: Set of integers Z
The set of integers Z = { .., -2, -1, 0, 1, 2, ... }
Definition 3: Set of rational numbers Q
The set of rational numbers Q = { a/b : where a,b ∈ Z }
Definition 4: ~
A~B if and only if there is a one-to-one correspondence between the elements of A and the elements of B.
Definition 5: Infinitely countable
A set S is said to be infinitely countable if there is a one-to-one correspondence between that set and the set N. That is, S~N.
Theorem 1: The union of two infinitely countable sets is infinitely countable
Proof:
(1) Let A be an infinitely countable set so that A~N
(2) Let B be an infinitely countable set so that B~N
(3) Let O be the set of odd positive integers = {1, 3, 5, ... }
(4) Let E be the set of even positive integers = {2, 4, 6, ... }
(5) N~O since we can map x to 2x-1 such that:
1 --> 1
2 --> 3
3 --> 5
...
(6) N~E since we can x to 2x such that:
1 --> 2
2 --> 4
3 -- > 6
...
(7) O + E = N ~ N
This is true since N consists of all the positive odd integers and all the positive even integers.
(8) A ~ O since A~N and O~N
(9) B ~ E since B~N and E~N
(10) A + B ~ A + B ~ O + E ~ N
QED
Corollary 1.1: The set of integers Z is countable
Proof:
(1) Let W = the set of positive integers = {0, 1, 2, 3, ... }
(2) W ~ N
In this case, x maps to x-1 so that we have:
1 --> 0
2 --> 1
3 --> 2
...
(3) Let Z-= the set of negative integers = {-1, -2, -3, ... }
(4) Z- ~ N
In this case, x maps -x so that we have:
1 --> -1
2 --> -2
3 --> -3
...
(5) Z = Z- + W so Z is countable because it is the union of two countable sets. [Using Theorem 1 above]
QED
Theorem 2: The set of ordered pairs WxW is infinitely countable
The set WxW is infinitely count where W={0, 1, 2, ... } and WxW = { (0,0), (0,1), ..., (1,0), (1,1), ..., (2,0), ... }
Proof:
(1) The trick here is to find a way of ordering WxW so that we can visit each ordered pair one-at-a-time and still be on track to visit all of them.
(2) Here's the ordering:
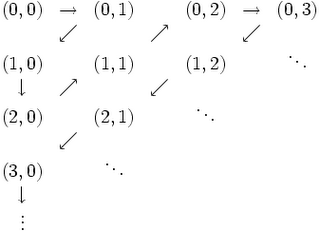
(3) We can see that all possible ordered pairs can be listed in this grid and the zig-zag traversal will eventually visit each one.
QED
Corollary 2.1: If two sets A,B are infinitely countable, then AxB is infinitely countable.
Proof:
(1) Since W ~ N, we can see that A ~W, B~W
(2) This means that AxB ~ WxW
(3) Since WxW ~ N [By Theorem 2 above], we have AxB ~ N.
QED
Theorem 3: All infinite subsets of an infinitely countable set are infinitely countable
Proof:
(1) Let A be an infinite set that is infinitely countable.
(2) Let B be an infinite subset of A.
(3) Now, by definition, we know that we can order the elements in A such that A = {a1, a2, ..., an }
(4) Now, it follows that B can be listed in the same way with deletions so that you have:
{aa, ab, ac, ... } where a is less than b is less than c etc.
(5) The mapping consists of traversing B in the same order as A so that you have:
1 --> aa [The first element in A not deleted]
2 --> ab [The second element in A not deleted]
3 --> ac [The third element in A not deleted]
...
QED
Theorem 3: The set of rational numbers is infinitely countable
Proof:
(1) The trick here is that we can allow repeats. We come up with an algorithm that will sequentially generate all the rational numbers that exist with repeats.
(2) We can use repeats since by Lemma 2 above, if Q + repeats is infinitely countable then its subset Q (deleting all the repeats) is infinitely countable.
(3) We can map rational numbers to Z x N where Z is the set of integers = { ..., -1, 0, 1, ... } and N is the set of natural numbers = {1,2,3,4, ... } since:
(a) Each rational number q = a/b where a,b ∈ Z. [Definition of rational numbers]
(b) We can assume b is a positive integer since:
b ≠ 0 [Since division by zero is not allowed] and if b ≤ -1, then a/b = (-a)/b where b ≥ 1.
(c) So, every q=a/b maps to (a,b) where a ∈ Z and b ∈ N.
(4) Since Z is infinitely countable (See Corollary 1.1 above) and N is infinitely countable (by definition), we know that ZxN is infinitely countable (By Corollary 2.1 above)
QED
Theorem 4: The number of real numbers between 0 and 1 is not infinitely countable
Proof:
(1) Assume that the real numbers between 0 and 1 is infinitely countable so that there is a mapping between these numbers and N.
(2) Then there should be a complete list. All real numbers would have to be included in this mapping.
(3) But it is possible to construct a number that is not one the list.
(4) All numbers in this list are of the form. 0.xxxxxxxxx....
(5) Let x1 = the first number in the list and x1,1 = the first digit of the first number in the list so that 0 ≤ x1,1 ≤ 9.
(6) Let n1 = any other digit. For example, if x1,1 = 9 then we could have n1 = 8.
(7) We can see that all numbers that we create from n will not equal x1
(8) Let x2,2 = the second digit of the second number on the list.
(9) We can now set n2 = any other digit so that n is now distinct from x1 and x2.
(10) We can continue doing this for as long as i and in each case n is different from all the real numbers that came up to i.
(11) In this way, it is possible to set n = a real number which is not on the list.
(12) But this is impossible since we assumed that there was a complete mapping. Therefore, we have a contradiction and we reject our assumption at step #1.
QED
Corollary 4.1: There are an uncountable number of real numbers.
Proof:
This follows directly from the theorem above since (0,1) is a subset of all real numbers so that if (0,1) is uncountable, it follows that the R, the superset of (0,1) is also uncountable.
QED
Corollary 4.2: The number of irrational numbers is uncountable
Proof:
(1) The set of real numbers = the set of rational numbers + the set of irrational numbers.
(2) The set of rational numbers is infinitely countable. [See Theorem 3 above]
(3) Assume that the set of irrational numbers is infinitely countable.
(4) Then the set of real numbers is infinitely countable since it is the union of the rational and the irrational numbers [See Theorem 1 above]
(5) But this contradicts Theorem 4 that the real numbers are not infinitely countable.
(6) Therefore, we have a contradiction and we reject our assumption in step #3.
QED
References
- Countable Set, Wikipedia
- Countability of the Rational Numbers, Cut-The-Knot
25 comments :
You are incorrect in stating that the real set (0,1) is uncountable. You can visit every number in the interval just as you illustrated with ordered pair example. Visit http://mathphile.blogspot.com/ for an explanation of this.
Thanks for you post. I read your blog and I accept your opinion as sincere.
Cantor's argument is that there is not a one-to-one correspondence between the natural numbers and the real numbers. In a nutshell, his argument is no matter how you try to list the real numbers, there will always be at least one that you are unable to include.
His argument applies to your traversal argument. Each number in your traversal could be numbered. In other words, there is a one-to-one correspondence between the natural numbers and your traversal. Still, using Cantor's argument, there will always be at least one real number that is not included in your traversal. In other words, no matter how close you get, there is still not a one-to-one correspondence between the (0,1) and the natural numbers. :-)
-Larry
Larry,
I have shown that you can list every real number in the interval [0,1]. Cantor's argument is incorrect. In plain language, Cantor was wrong. You say there will be a number that is not in my list? Please state one number you think is not in my list and I will show you that it is in my list. :-) My list employs simple combinatoric logic that includes all possible numbers in the real interval [0,1].
To be clearer, the missing link in your argument is the proof that your algorithm is complete with respect to the real set (0,1).
Numbers that I suspect are not in your list:
(π - 3)
(sqrt(2) - 1)
(e - 2)
If I'm wrong, show me your number. :-)
Here's a link that addresses the underlying assumption in your proof. If Cantor's argument works for rationals, why doesn't it also work for reals.
Cheers,
-Larry
Larry,
pi-3, e-2 and sqrt(2)-1 are all in my list. You write:
"To be clearer, the missing link in your argument is the proof that your algorithm is complete with respect to the real set (0,1)."
I have no idea what you are trying to say here. My argument has no missing link. It is 100% solid. Care to explain what you mean?
The tree structure I use as an illustration contains each and every real number in the set (0,1). There are no exceptions, including the numbers you suggested are not in my list. In fact, they are in the list and it is very easy to verify. Simply follow the correct path starting with the first digit since every possible permutation is taken into account.
Hi John,
Sorry if my comment about the "missing link" wasn't clear.
I will try now to make this point clearer. I will show a criteria for proving that a set is countable, show that integers and rationals meet this criteria, and then show that your "tree traversal" of the decimals does not.
I want to thank you for asking me to more clearly state my argument. I hope that you find the following definition and lemmas interesting. :-)
Definition 1: Countable Set
(1) A set C is countable if there is a one-to-one correspondence between its elements and the whole numbers {1, 2, 3,...}
Lemma 1: Criteria for a Countable Set
A set C is countable if and only if there exists an ordering O such that for any element c of C, there exists a whole number i such that O(i) = c.
Proof:
(1) Assume that an ordering exists as described in the hypothesis.
(2) Clearly, then, there is a mapping between the whole numbers and the elements of the set C and by the definition, the set C is countable.
(3) Assume that no ordering exists.
(4) Assume further that a set C is countable.
(5) But if a set C is countable, then there exists a mapping between the whole numbers and the set C.
(6) But this is impossible since we assumed in step #3 that no such ordering exists.
(7) Therefore we have a contradiction and we reject our assumption in step #4.
QED
Lemma 2: The set of integers Z is countable
(1) We can define an ordering O such that:
1: 0
2: 1
3: -1
4: 2
5: -2
...
(2) Then, for any integer x, we can define the following function:
if x > 0, then i=2*x
if x < 1, then i=2*x+1
(3) This then gives us:
Then x=O(i)
(4) So, using Lemma 1 above we can conclude that the integers are countable.
QED
Lemma 3: The set of rational numbers Q is countable.
(1) We construct a table with the following set of numbers at the top which I will call "column value"
1, -1, 2, -2, 3, -3, 4, -4, ...
We can likewise label each row:
1, 2, 3, 4, 5, ...
which I will call the "row value"
Now this table can be traversed in the following way:
1) Write 0
2) Set column = 1, row = 1, direction = 0; write 1
3) If direction = 0, then row=row+1, direction=up, write (column value)/(row value)
4) If direction = up and row not = 1, then row = row - 1; column = column + 1; write (column value)/(row value)
5) If direction = up and row = 1, then column = column + 1, direction = down; write (column value)/(row value)
6) If direction = down and column not = 1, then row = row + 1; column = column - 1; write (column value)/(row value)
7) If direction = down and column = 1, then row = row + 1; direction = up; write (column value)/(row value)
8) Go to step #4
(2) We can define an ordering O using the traversal above to get:
1: 0
2: 1
3: 1/2
4: -1
5: 2
6: -1/2
7: 1/3
...
(3) For 0, i = 1, so we can assume that a/b is nonzero.
(4) For any nonzero rational number a/b, we know that:
row = b
to figure out the column:
if a > 0, then column = 2a-1.
if a < 0, then column = 2a
(5) Now, it is clear that there exists some i where this column and row is reached that can be calculated.
For example, for column =3, row =3, i = 14.
(6) So, using Lemma 1 above we can conclude that the rational numbers are countable.
QED
Lemma 4: The ordering of (0,1) using decimals does not prove that (0,1) is countable.
(1) Let us define the following ordering (assume that this matches the tree traversal of decimals that you propose):
0.1
...
0.9
0.01
0.02
...
0.09
0.11
...
0.19
0.21
...
0.001
...
So for example:
O(1) = 0.1
O(9) = 0.9
etc.
(2) It is clear that for all i, O(i) is a terminating decimal
(3) This means that for nonterminating decimals such as 1/3 or for irrational numbers such (π - 1), there is no i such that O(i) = 1/3 or O(i) = (π - 1).
(4) Since not all reals in (0,1) have an i associated with them, using Lemma 1 above, this shows that O(i) is not a one-to-one correspondence between the reals in (0,1) and the whole numbers.
QED
Hi Larry,
You wrote:
"This means that for nonterminating decimals such as 1/3 or for irrational numbers such (π - 1), there is no i such that O(i) = 1/3 or O(i) = (π - 1)."
But of course there is an i for 1/3! (and all the others). There is an i such that O(i) is an element of (0,1) for 'every' real number in the set (0,1). You do not know the i except that it exists. This should not surprise you because you cannot know the i in general, only that it exists. All you know is that the first i is 0 such that O(0)=0.0. You do not need to know the rest of the i's because this information is irrelevant.
The fact that you cannot write 1/3 in a finite form does not negate this argument in any way. In considering the countability of the rationals, you cannot write 1/3 completely in any radix form but it does not detract from the validity of the argument.
Hi John,
Well, I think we have found the difference between your thinking and the standard view of mathematicians.
If you stick to your ordering algorithm or for that matter, any ordering algorithm variant, you can decide on the first element, true, or the first n elements, etc., but there will always be nonterminating decimals that your algorithm does not cover
The standard view of mathematicians , as I understand it, is that your ordering algorithm is not a true one-to-one correspondence so it is not a proof of countability.
Your view, as I understand it, is that as long as you can select any specific nonterminating decimal and place it at the beginning of the algorithm (as Cantor placed 0 at the beginning of his ordering of rationals) and as long as the nonterminating decimal consists of the standard decimals, then you feel that you have established a one-to-one correspondence.
I think, then, that our discussion is over. Please feel free to let me know if I have misunderstood your viewpoint.
-Larry
There is no difference between my view and that of other mathematicians, that is, I am drawing conclusions from Cantor's definition of countability.
You wrote:
“....but there will always be nonterminating decimals that your algorithm does not cover.”
Not so, my algorithm covers every real number in the interval [0,1] whether it be terminating or nonterminating. It is also a 'true' one-to-one correspondence and the ordering is of no importance – I stated you would not be able to write the numbers sequentially and of course this is immaterial.
You wrote:
“Your view, as I understand it, is that as long as you can select any specific nonterminating decimal and place it at the beginning of the algorithm (as Cantor placed 0 at the beginning of his ordering of rationals) and as long as the nonterminating decimal consists of the standard decimals, then you feel that you have established a one-to-one correspondence.”
Not entirely correct. You have to start at the beginning Larry because it's the only logical place to start. In Cantor's example, he also starts at the beginning. By the way, I have no idea what you mean by 'standard decimals' ? Are there non-standard decimals? Never heard of these.
Look, what I am saying is that Cantor's ideas are not entirely correct. Especially his ideas on different infinities – this is absolute nonsense. I have also shown that his statement regarding the countability of the real interval [0,1] is false according to his definition.
John
Hi John,
To be even clearer, to prove a 1:1 correspondence between (0,1) and the whole numbers you need to do the following:
(1) Clearly and precisely state the ordering algorithm.
In other words, anyone other than you who understands the algorithm, at point i, will state the same real as you.
In my view, you state an algorithm such as 0.1, 0.2, ..., 0.9, 0.01, .., 0.09, 0.11, ... so you meet this requirement.
If I am misunderstanding your algorithm, let me know.
(2) After stating the algorithm, it should be possible to pick any real number r and identify a whole number i such that O(i) = r.
This is where you ordering fails. If the decimals are always terminated, there is NEVER an i where O(i) = a nonterminating fraction (such as 1/3) or where O(i) = an irrational (such as π - 3).
If you restate your algorithm to be a list of reals, that's fine, but I am always free to pick another one that is not already in your list. So, I am free to use Cantor's diagonal argument to always come up with a number that is not in your list.
So, either you try to list out the irrationals and you will fail by Cantor's Diagonal or you use your algorithm and there is no i where O(i) = a nonterminating decimal.
It's not enough to say that it doesn't matter. In that case, you are changing the requirements for a 1-to-one correspondence.
(3) Finally, even if you are able to show that your algorithm covers all the nonterminating decimals that I come up with, you still need to prove that a whole number i eventually exists for ALL real numbers: both rational and irrational.
The proof here can be inductive or it can be a proof by contradiction or any other type of logical argument but it must be a proof.
It must include the assumptions of the proof, definitions if necessary , postulates, and then finally the step-by-step proof. Assertions are not a proof.
I think that if you try such a proof of completeness, you will quickly see that your ordering algorithm is not complete.
From my view, you have proven that there are a countable number of terminating decimals but you have not proven that there are a countable number of nonterminating decimals (irrationals + certain fractions such as 1/3).
-Larry
For a given set S and a bijective
function O such that
O:S->N (N = natural numbers)
we say that S is called countably
infinite or denumerable.
This is Cantor's definition and it states nothing about
'ordering' so ordering is not important.
You claim that I cannot find an i such that O(i)=1/3. But take note that this is NOT what the definition states. Rather it states that given 1/3, then O(1/3) = i. Of course we cannot find this i and according to the definition it is sufficient to prove that such an i exists even though we don't care about its value.
In my algorithm, I clearly show that such an i must exist for all the real numbers in [0,1] - this is sufficient to complete the proof. I do not need to find this i; only to know that it 'exists'.
If I can construct 1/3 using my algorithm, then I have effectively proved that such an i must exist.
So examining the case of 1/3, we start at 0.3 and follow the tree choosing 3 in each new branch. Continuing in this fashion we construct a value that will become indistinguishable from 0.333... Thus the fact that we can write down and count each new number formed, proves the set [0,1] is countable and we are done.
See, I think you may be confused when you think about 1/3 in terms of base 10. For example, if I used base 3 instead of base 10, then 1/3 would equal 0.1 which is finite and I would have that O(1/3) = 2 so that if f is a function that takes N to O, then I would have that f(2)=0.1 or f(2)=1/3. You cannot allow the nonterminating representation of 1/3 in base 10 or pi-3 or sqrt(2)-1 or any other real number representation in base 10 to throw you off. Does this make sense to you?
Any mapping between a set and the whole numbers is an ordering (you have a number associated with 1, a number associated with 2, etc.)
A bijective function is just a 1:1 correspondence which means that not only is there an O(#) = i but there must also be an i such that O(i) = #. Granted, proving a correspondence with a subset of the whole numbers would work but your algorithm implies a mapping with the complete set of whole numbers (there is a clear sense of the first number, the second number, etc.)
You can specify any base you want but you cannot claim more than one base as part of your ordering. If you are claiming base 3, then yes, 1/3 becomes a terminating number, but other fractions become nonterminating such as 1/2.
You are correct that it is sufficient to prove that i exists but you don't do this. In fact, it is clear that all i's are terminating (regardless of the base) so no i exists which is nonterminating for that base and no i ever exists for an irrational number. Since for your algorithm, there is no associated i for certain numbers, it follows that your algorithm does not prove a 1:1 mapping between (0,1) and N.
-Larry
You state:
"A bijective function is just a 1:1 correspondence which means that not only is there an O(#) = i but there must also be an i such that O(i) = #."
Well, consider f(x) = sqrt(x). This is bijective as long as x >= 0. Now if f(x)= 2.82842..., then can you tell me what x is? The answer is NO. However, there is an O(#)=i and O_inverse(i) = #. In this case you
can only give me an approximation. So Larry, whatever your argument is regarding finding an i, it
does not matter in my proof. Ordering does not matter because it is not part of the Cantor definition.
"You are correct that it is sufficient to prove that i exists but you don't do this."
But Larry, I do exactly this: this is what my tree diagram proves. I have shown that you can
represent EVERY possible decimal number in the interval [0,1] using my tree diagram. This is
sufficient proof. You talk about i being non-terminating or terminating but i is ALWAYS finite, that
is, it is a NATURAL number. It is O(i) that is either terminating or non-terminating. Once again,
i is a natural number.
"Since for your algorithm, there is no associated i for certain numbers, it follows that your
algorithm does not prove a 1:1 mapping between (0,1) and N."
Not so. I challenged you to provide one such number but you were not able.
You wrote that pi-3, sqrt(2)-1 and e-2 were numbers that I could not find an i for.
And of course you are correct BUT as I explained, I do not need to find an i for
any of these numbers, suffice to show that an i EXISTS. How can you show that
an i exists? Simple: if my function O(i) = pi-3 then provided I can show that pi-3 is
"a number in my list", I have completed the proof. Now it is easy to see that pi-3
is in my list. Ergo, I have nothing further to add.
Hello,
As a quick aside, I would just like to thank Mr. Freeman for this blog. It has helped me through some rough spots in learning the basics of real analysis.
I have to agree with him on this point. Cantor was right. Although your tree diagram had me a little worried, the way you have defined the mapping, only terminating decimals are mapped. You can map 0.3,0.33, 0.333, even "0." followed by 10^23 3s. But you never map any nonterminating decimal. By stopping at places along the tree diagram, you have set up a generating function that, by definition, stops after a finite number of decimal spots. Although 1/3 is in your list, it is never mapped by a natural number.
Hope that makes some sense...
Anonymous,
You write:
"Although your tree diagram had me a little worried, the way you have defined the mapping, only terminating decimals are mapped."
My response: What makes you think this? All decimals are mapped - both terminating and non-terminating. I do not 'stop' anywhere on the tree except to increment my counter for the decimal represented at that point.
There is no generating function as you incorrectly presume. All the numbers in the interval [0,1] are represented.
You write:
"Although 1/3 is in your list, it is never mapped by a natural number."
My response: 1/3 does not have to be mapped. It is sufficient that it exists in the list. Besides, 1/3 is not representable in decimal (I am not going to argue about this). If I were to build this tree in base 3, 1/3 would be mapped. So your argument about mapping is irrelevent. We care only that a number is in the list and we can visit this number exactly once in our traversal. It does not matter when we visit it, only that we visit it once - whenever. Does this help you? Cantor was not only wrong but he was a fool.
Hi John,
In my view, you have not succeeded in establishing some of your statements.
For example, you write:
"All decimals are mapped - both terminating and non-terminating. I do not 'stop' anywhere on the tree except to increment my counter for the decimal represented at that point."
But what do you mean by "mapped"? In my Criteria for a Countable Set (Lemma 1), I provide a mechanism for establishing mapped which contradicts your approach.
If you reject my Criteria, then you need to provide a criteria of your own and provide an example of a set that doesn't meet your criteria.
For example, if I have three tokens and four items, there is clearly not a 1-to-1 mapping. If I assign all three tokens to one and only one item, then for one item there is no token. If there is a one-to-one mapping (as is the case of 3 tokens and 3 items), then for any item, I can find a definite token and for every token, there is a definite item.
You write:
"I do not 'stop' anywhere on the tree except to increment my counter for the decimal represented at that point."
But that's exactly the issue. In a 1-to-1 mapping, there is always a stop. There is always a definite place on the tree where the mapping exists.
You write further:
"We care only that a number is in the list and we can visit this number exactly once in our traversal. It does not matter when we visit it, only that we visit it once - whenever."
If you say that it "eventually exists" or that you are assuming "everything that will possibly occur", you are talking about items that will never be in the set.
Saying that a nonterminating decimal is included in your tree is a bit like saying that infinity is included in the list of integers. We know that infinity exists (that's the number of integers there are) and using integers, we can get as close as we like without getting there (assuming that 1000 is closer to infinity then say 10) By your logic, the integers have a highest number: infinity.
But this is incorrect. There is no highest integer. Infinity is not an integer.
Are you willing to now argue that infinity is an integer or are you willing to concede that certain numbers (in this case, nonterminating decimals) are always outside the set of generated values.
I don't feel that your argument about bases work. Yes, in Base 3, 1/3 becomes a terminating decimal. But in Base 3, 1/2 becomes a nonterminating decimal. Regardless of which base you choose, there are always nonterminating decimals and it is these nonterminating decimals that show that the real numbers are not countable.
-Larry
Larry,
For the life of me, I am trying to understand how it is you cannot see my arguments.
What do I mean by mapped? Well, if you perform the traversal I suggested, then every real number in the interval [0,1] is mapped to a natural number. You start the first mapping as follows:
For the first top-down traversal:
f(1) = 0.0
f(2) = 0.1
f(3) = 0.2
f(4) = 0.3
...
f(10) = 0.9
For the second top-down traversal:
f(11) = 0.00
f(12) = 0.01
f(13) = 0.02
...
f(20) = 0.09
f(21) = 0.10
f(22) = 0.11 ....
Do you get the idea?
Every real number in the interval is mapped to a natural number.
Now back to my first question - where is there a disconnect in your understanding? I think the process of 'stopping' is causing confusion. What I meant by stopping, is that one can map each real number to a natural number and proceed to the next number that is mapped. In so doing, you are able to visit every number in the interval. It does not matter if it takes you forever! It would take you forever to do this with rational numbers also or with any other set that is infinitly countable.
My argument about 'bases' is valid. Why? If it is not valid, then the rational numbers are also uncountable according to your argument. Larry, repeating or non-repeating decimals do not factor into any of the arguments. It does not matter how you choose to represent a number in the interval [0,1] - only that you CAN represent it.
There is yet one more thing I want to clarify: it is not possible to write down every real number, but does this matter? Of course NOT! You cannot write down every rational number either. It would take you forever just to write down the numbers. From my tree diagram, you can see that if you live forever, you can carry on writing down each number forever and ever. Writing down the numbers is not important. You can't do this with any of the other sets you consider countable. What is important, is that you can visit each of these numbers and map each to a natural number - this is Cantor's definition. You can do this with the real interval (0,1).
Hi John,
I will do my best to explain my view.
First, let me be clear on what you do succeed in arguing:
(1) For any real number between 0 and 1, it is possible to select a base such that the real number is representable by a finite decimal.
For 1/3, the base is 3 and the representation is 0.1 in base 3.
For (pi - 3), the base could be (pi - 3)^(-1) and the representation would be 0.1.
In fact, any number given the selection of the appropriate base can be represented as 0.1.
(2) Any finite decimal is countable.
I think that this point is pretty clear.
Here are the problems with your logic in my opinion:
(*1) All countability arguments are relative a specific base.
Countability is always relative a specific base. It is true that you can pick any base you want but for any base selected, there will always be real numbers that are nonterminating for that base.
For base 10, 1/3 is nonterminating. For base 3, 1/2 is nonterminating.
2) The existence of a nonterminating decimal shows that the real numbers are not countable.
This is the argument that I made before. To prove something is countable, you can pick any ordering you want but you must show that each point in the set is reached in a finite amount of steps.
In other words, a countable infinity is an infinite set (there's always one more item no matter how many you remove) that is also countable (any item in the set is reached after a certain integer number of steps).
So, if you pick your base (let's say 10), it turns out that values like pi - 3 will never be reached using your algorithm.
If you pick a (pi - 3) friendly base, I would suspect that values like 1/2 or 1/3 will never be eached.
No matter which base you select, there will be certain values that are not reached in a finite number of steps.
You write:
"It does not matter if it takes you forever! It would take you forever to do this with rational numbers also or with any other set that is infinitly countable."
I'm sorry but this is not correct. If it takes you "forever", then it is not taking a finite amount of steps and it is not countable.
You are not correct about the rational numbers. Take any rational number you like. Using Cantor's algorithm, it is possible to determine the number of steps before the rational number is reached. It might be a very high number but it will never be forever and it will always be a finite number of steps to that rational number. That's why the rational numbers are countable.
You write:
"...but you must show that each point in the set is reached in a finite amount of steps."
Where in the definition of countability do you see anything about a 'finite amount of steps'?
As for rational numbers, you are correct in stating that a rational number can be reached in a finite amount of steps unless it is a recurring number, in which case your argument fails.
Countability means a one-to-one mapping with the whole numbers. For any element of a countable set, there must be an associated finite number. A finite number is always reachable in a finite number of steps of +1.
All rational numbers can be expressed in the form of a/b where a,b are integers (see Definition 3 above). Using Cantor's argument (see Lemma 3 above), it is possible to associate any a/b with a finite number i.
-Larry
Larry,
You use the term 'finite number' but you have not defined it. All numbers are 'finite'.
You write:
"All rational numbers can be expressed in the form of a/b where a,b are integers (see Definition 3 above). Using Cantor's argument (see Lemma 3 above), it is possible to associate any a/b with a finite number i."
It is also possible to associate all irrational numbers with a number i as I have already demonstrated in my tree diagram. How is this any different from what you are saying?
By "finite number," I mean an element of N where N is set of natural numbers: 0, 1, ...
1,000,000,000 is an element of N so it is a "finite number". Infinity is not an element of N.
I've already stated to my own satisfaction why the set of irrational numbers is not one-to-one with the set of N so I won't bother to repeat it.
If this does not convince you even as I have responded to each of your arguments, then I am at a loss for what else I should say.
Larry,
It is only possible to associate a/b with any natural number
i provided you avoid using radix representation. However, this
is exactly the problem: Cantor uses base 10 in his diagonal
argument. How can you associate 1/3 with some i if it (1/3) is
not finitely represented? Why, there is even a contradiction here
because the Cantor tree diagram assumes all real numbers (0,1)
are in the list!
Sorry Larry, Cantor was a fool who was transparent to his
peers.
John
An irrefutable proof that real numbers do not exist:
http://www.spacetimeandtheuniverse.com/math/4507-0-999-equal-one-317.html#post21409
Hence Cantor was an idiot.
All Cantor's Delusions (and much more) exposed here:
http://www.spacetimeandtheuniverse.com/math/4507-0-999-equal-one-556.html#post27247
Post a Comment