In a previous blogs, I reviewed the foundations of derivatives and some of their advanced properties. In today's blog, I will examine the area under the curve problem and show how definite integrals solve this problem.
The content in today's blog is largely taken from the Wikipedia article on Riemann sums and Edwards and Penney's textbook Calculus and Analytic Geometry.
For purposes of today's blog, I will use the example of the curve f(x) = x3. I will focus on the problem of determining the area under the curve between x=0 and x=2 and y=0. The question at hand is how do we figure out a general method for determining the the total area within these constraints:

One approach to this problem to use a Riemann sum. Reimann sums were first proposed by Bernhard Riemann and today they are a major part of the foundation of calculus.
Now, let me offer a formal definition of a Riemann sum. If you are not interested in formal definitions, feel free to skip this. I will include a more intuitive summary afterwards.
Definition 1: Partition
Let I = [a,b] be a closed interval. [See Definition 3, here for definition of closed interval]
A set P is said to be a partition of I if P is a set of nonempty subintervals = { [a,x1) [x1, x2), ... , [xn-1,b] } where n, the number of subintervals, is a positive integer and a is less than x1 which is less than x2 ... which is less than xn-1 which is less than b.
Definition 2: Riemann sum
Let f(x) be a real value function on a closed interval I=[a,b] such that f: I → R. Let P be a partition of the interval I.
The Riemann sum S of f over I with respect to a partition P is:
S = ∑ (j=1,n) f(cj)(xj - xj-1)
where cj is any arbitrary point in [xj, xj-1].
If cj = the minimum in [xj, xj-1] for all j, then S is a lower Riemann sum which I will denote as L(P)
If cj = the maximum in [xj, xj-1] for all j, then S is an upper Riemann sum which I will denote as U(P).
The important idea here is that a Riemann sum consists of dividing up a the graph of a function into an arbitrary number of intervals.
Here's a diagram of an upper Riemann sum U(P) where the rectangle corresponds with the maximum point in the interval.
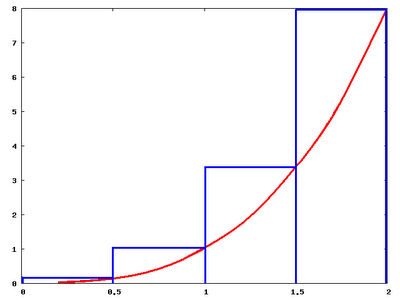
Here is a diagram of a lower Riemann sum L(P) where the rectangle corresponds with the minimum point in the interval.
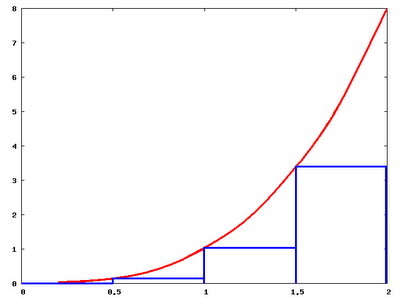
Now, it should be clear that as we increase the number of subintervals in a partition, both the L(P) and U(P) get closer to the true area under the curve. In fact, we have hit our answer when U(P) = L(P).
The goal of the rest of this blog is to demonstrate that if we continue to increase the number of subintervals, we eventually get to this point. Then, I use Riemann sums to determine the area under the curve where f(x) = x3.
Lemma 1: For any partition P of [a,b], L(P) ≤ R(P) ≤ U(P)
Proof:
(1) Let f(pj) be the minimum point in each interval [xj, xj-1]
(2) Let f(qj) be the maximum point in each interval [xj, xj-1]
(3) It follows that for all j, f(pj) ≤ f(qj).
(4) It therefore follows that for all j, f(pj)(xj - xj-1) ≤ f(qj)(xj - xj-1).
(5) And therefore that ∑ (j=1, n)f(pj)(xj - xj-1) ≤ ∑ (j=1,n)f(qj)(xj - xj-1).
(6) It follows that L(P) ≤ R(P) ≤ U(P) since for all j, f(pj) ≤ f(cj) ≤ f(qj).
(7) Applying the same steps as before (step #4 and step #5), we can conclude that:
L(P) ≤ R(P) ≤ U(P)
QED
What makes Riemann sums interesting, is that for any partition P, it is possible refine it. That is, we can increase the number of partitions and get an answer that it closer to the true area under the curve.
Definition 3: Refinement of a Partition
A partition P' is said to be a refinement of a partition P if and only if each subinterval of P' is contained in some subinterval of P.
In other words, each interval in P now corresponds to a unique set of one or more intervals in P' and the total number of intervals in P' is greater or equal to the total number of intervals in P.
Lemma 2: If P' is a refinement of P, then L(P) ≤ L(P') ≤ U(P') ≤ U(P)
Proof:
(1) From Lemma 1 above, we know that:
L(P') ≤ U(P') and L(P) ≤ U(P).
(2) Assume that a partition P' is derived from a partition P by dividing up the kth subinterval [xk-1, xk] of P into [xk-1,z] and [z, xk] by introducing a point z.
(3) From this perspective, the only difference between L(P) and L(P') is that the term f(pk)*(xk - xk-1) is now replaced by:
f(u)*(z - xk-1) + f(v)*(xk - z) where u,v are the minimum points on [xk-1,z] and [z, xk] respectively.
If we set L'(P) = L(P) - f(pk)*(xk - xk-1), then we have:
L(P) = L'(P) + f(pk)*(xk - xk-1)
L(P') = L'(P) + f(u)*(z - xk-1) + f(v)*(xk - z)
(4) Since f(pk) is the minimum point for all (xk-1, xk), we have:
f(pk) ≤ f(u)
f(pk) ≤ f(v)
(5) Hence, it follows that:
f(u)*(z - xk-1) + f(v)*(xk - z) ≥ f(pk)*(z - xk-1) + f(pk)*(xk - z) = f(pk)*(z - xk-1 + xk - z) = f(pk)*(xk - xk-1)
(6) From step #3, we have :
L'(P) + f(u)*(z - xk-1) + f(v)*(xk - z) ≥ L'(P) + f(pk)*(xk - xk-1)
So that:
L(P') ≥ L(P)
(7) We can use the same exact reasoning to establish that U(P') ≤ U(P).
(8) So that we have:
L(P) ≤ L(P') [step #6]
L(P') ≤ U(P') [Lemma 1 above]
U(P') ≤ U(P) [Step #7]
QED
Lemma 3: Limit to the lower Riemann sum
Let Pn denote a partition P of the interval [a,b] such that P consists of 2n subintervals of equal length.
Then, there exists a value I = lim (n → ∞) L(Pn)
Proof:
(1) By Definition 3 above, each Pn+1 is a refinement of Pn.
(2) Using Lemma 2 above:
L(P1) ≤ L(P2) ≤ ... ≤ L(Pn) ≤ ...
(3) The sequence { L(Pn) } is a nondecreasing monotonic sequence of real numbers. [See Definition 8, here for a definition of nondecreasing monotonic sequence]
(4) The sequence is clearly bounded since:
(a) Let D = the minimum value of f on [a,b] (See Theorem, here for proof that a minimum exists)
(b) Let U = the maximum value of f on [a,b] (See Lemma 3, here for a proof that the maximum exists)
(c) Since L(Pn) = ∑ (i = 1, 2n) f(pi)(xi - xi-1), it is clear that:
U*(b-a) ≤ L(Pn) ≤ M*(b - a)
(5) Therefore, I must exist since a bounded monotone sequence of real numbers must converge. [See Lemma 1, here]
QED
Definition 4: mesh(P)
The mesh of a partition P is the largest length of xi - xi-1.
If all the subintervals that make up the Riemann sum are the same, then mesh(P) = this value. If they are not the same, then mesh(P) = the largest subinterval.
Lemma 4:
For any given real ε greater than 0, there exists a real δ greater than 0 such that if P is a partition of [a,b] with mesh(P) less than δ and P' is a refinement of P, then:
abs(L(P) - U(P)) is less than ε/3 and abs(R(P) - R(P')) is less than ε/3
for any two Riemann sums R(P) associated with P and R(P') associated with P'.
Proof:
(1) Let f be a continous function on the closed interval [a,b]
(2) Since [a,b] is bounded and closed, [a,b] is compact. [See Heine-Borel Theorem, here]
(3) Since [a,b] is compact, f is uniformly continuous on [a,b]. [See Heine-Cantor Theorem, here]
(4) So, there exists a number δ greater than 0 such that if:
abs(u - v) is less than δ, then abs(f(u) - f(v)) is less than ε/[3(b - a)]. [See Definition 1, here for definition of uniformly continuous functions]
(5) Suppose now that P is a partion of [a,b] with mesh(P) less than δ.
(6) Then, abs(U(P) - L(P)) = ∑ (i=1,n) abs(f(qi) - f(pi))Δxi which is less than ε/[3(b-a)]∑(i=1,n) Δxi = ε/3 [Since ∑(i=1,n) Δxi= (b - a)].
This is valid since abs(pi - qi) is less than δ since mesh(P) is less than δ and pi and qi belong to the same interval.
(7) By Lemma 1 above, L(P) ≤ R(P) ≤ U(P) where R(P) = any Riemann sum and this is also true of L(P') ≤ R(P') ≤ U(P') where P' is a refinement of P.
(8) By Lemma 2 above, L(P) ≤ L(P') ≤ U(P') ≤ U(P).
(9) Combining #7 and #8, we can see that R(P) and R(P') are both within the interval [L(P), U(P)] which means that abs(R(P) - R(P')) is less than ε/3 since abs(U(P) - L(P)) is less than ε/3 [From step #6]
QED
This leads us to a definition of a definite integral.
Definition 5: Definite Integral (or Riemann Integral)
∫(a,b) f(x)dx = lim (n → ∞) ∑ (j=1,n) f(cj)(xj - xj-1)
I will try to explain each part of the definition since it is very formal. The ∫ is the notation introduced by Leibniz to indicate the sum of a continuous function (as opposed to ∑ which is the sum of a discrete set of values).
The (a,b) is the closed interval of the integral. The a should really be at the top of the ∫ and the b at the bottom but I am stuck with the limitations of html so this is the notation that I use.
dx is Leibniz's notation for Δx. The idea here is that the integral is the sum of rectangles, that is, an infinitely small width (dx) multiplied with the height f(x) as x varies from a to b.
Putting this together just says the "sum of the continuous function in the closed interval [a,b]".
So, we are defining the integral to mean the limit of the Reimann sum as the partition mesh gets closer and closer to 0.
Lemma 5: abs(a + b) ≤ abs(a) + abs(b)
Proof:
(1) if a,b are both nonegative, then abs(a + b) = a + b = abs(a) + abs(b).
(2) if both are both negative, then abs(a + b) = -(a + b) = -a + -b = abs(a) + abs(b)
(3) if a+b is positive and a is negative, then abs(a + b) = b - a is less than b + (-a) = abs(b) + abs(a) [We can make a parallel argument if a+b is positive and b is negative]
(4) if a+ b is negative and b is positive, then abs(a + b) = -(a + b) = -a -b = abs(a) - abs(b) which is less than abs(a) + abs(b). [We can make a parallel argument if a+b is negative and a is positive]
QED
Corollary 5.1: abs(a + b + ....) ≤ abs(a) + abs(b) + ...
Proof:
(1) We know that abs(a1 + a2) ≤ abs(a1) + abs(a2) from Lemma 5 above.
(2) Assume that it is true for up to some n so that we have:
abs(a1 + a2 + ... + an) ≤ abs(a1) + abs(a2) + ... + abs(an)
(3) Let b = a1 + a2 + ... + an
(4) abs(b + an+1) ≤ abs(b) + abs(an+1) [From Lemma 5 above]
(5) Replacing b with a1 + a2 + ... + an gives us:
abs(a1 + a2 + ... + an + an+1) ≤ abs(a1) + abs(a2) + ... + abs(an) + abs(an+1)
QED
Theorem: For any continuous function, the Riemann sum converges to the area under the curve.
Let I = the area under the curve. Let f be a function continuous on the closed interval [a,b]
For any positive real ε, there exists a positive real δ such that if P is a partition on f in [a,b] such that the mesh(P) is less than δ, then abs(I - R(P)) is less than ε where R(P) = the Riemann sum based on partition P.
Proof:
(1) Let ε be a real greater than 0.
(2) Let δ be a real greater than 0 based on the Lemma 4 above.
(3) By Lemma 3 above, there exists a δ2 such that there if we find an n such that mesh(Pn) is less than min(δ,δ2), then abs(L(Pn) - I) ≤ ε/3.
(4) Let P = Pn and let P' be a refinement on P.
(5) Then, abs(R(P) - R(P')) ≤ ε/3. [From Lemma 4 above]
(6) Further, since R(P') is in between L(P') and U(P') [from Lemma 1 above] and L(P) ≤ L(P') ≤ U(P') ≤ U(P) [from Lemma 2 above], it follows that:
abs(L(P) - R(P')) ≤ abs(L(P) - U(P)) ≤ ε/3 [From Lemma 4 above]
(7) abs(I - R(P)) = abs(I - L(P) + L(P) - R(P') + R(P') - R(P))
(8) Using Corollary 5.1 above, we have:
abs(I - L(P) + L(P) - R(P') + R(P') - R(P)) ≤ abs(I - L(P)) + abs(L(P) - R(P')) + abs(R(P') - R(P))
(9) Since abs(I - L(P)) is less than ε/3 [step #3 since P = Pn] and abs(L(P) - R(P')) is less than ε/3 [step #6] and abs(R(P') - R(P)) is less than ε/3 [step #5], we have:
abs(I - R(P)) is less than abs(I - L(P)) + abs(L(P) - R(P')) + abs(R(P') - R(P)) which is less than ε/3 + ε/3 + ε/3 = ε
QED
Example: Using a Riemann sum to estimate the area under f(x) = x3 on the closed interval [0,b]
(1) Using the definition of a Riemann sum, we can now use the Theorem above to get:
∫(0,b) f(x)dx = lim (n → ∞) ∑ (i=1,n) f(ci)Δx
(2) If we divide up P into n equal subintervals, then we can set Δx = b/n and set ci = ib/n. This then gives us:
∫(0,b) x3dx=lim (n → ∞) ∑ (i=1,n) (ib/n)3(b/n) = lim (n → ∞) ∑(i=1,n)(i3b4/n4)
(3) Since b,n are constants, we have:
lim (n → ∞) (i3b4/n4) = lim (n → ∞) (b4/n4) ∑(i=1,n)(i3)
(4) Using Lemma 4, here,
lim (n → ∞) (b4/n4) ∑(i=1,n)(i3) =lim (n → ∞) (b4/n4)[(1/4)n4 + (1/2)n3 + (1/4)n2]=
= lim (n → ∞) (b4)[(1/4) + (1/2)/n + (1/4)/n2]
(5) Since n is approaching ∞, this means that:
(1/2)/n and (1/4)/n2 approach 0 giving us:
lim (n → ∞) (b4)[(1/4) + (1/2)/n + (1/4)/n2] = b4/4.
This example shows the limitation of using Riemann sums to determine the integral. It makes a lot of sense as an explanation of how the integral relates to a limit. It presents problems when it comes down to applying it to a more general set of equations. If a summation formula exists, then the Riemann sum works fine. If a summation formula does not exist, then the Riemann sum, by itself, does not get us to a final result.
A much more powerful method for determining integrals is to view them as antiderivatives. That is, take the inverse of the derivative and the answer is the integral. How do we know that this works? This very important result is called the Fundamental Theorem of Calculus and I will go over its proof in my next blog.
References
- Riemann Sum, Wikipedia
- Riemann Sum, PlanetMath.org
- Edwards & Penney, Calculus and Analytic Geometry
No comments :
Post a Comment