Cofactor Expansion

In today's blog, I provide a general method for computing the determinant using cofactor expansion. This is taken from Matrices and Linear Transformations by Charles G. Cullen.

Lemma 1R:

If the rows of an n x n matrix A are linearly dependent, det(A)=0

Proof:

(1) Let A be an n x n matrix with rows that are linearly dependent.

[See Definition 1, here for review of linearly independent]

(2) Then, there exists α_i such that:

α₁R₁ + ... + α_nR_n = 0.

(3) Then, it is possible to use elementary operations to set R₁ = 0 since:

(a) Multiply R₁ with α₁

(b) For each row i (where i = 2 .. n), add α_i*R_i to R₁.

(c) By step #2, it is clear after (a) and after each addition (b), R₁ = 0.

(4) So we have:

A_(0R1) = E_nE_n-1...E₂E₁A where E_i is an elementary operation. [See Theorem 5, here for review of how elementary operations map to multiplication]

(5) Using the definition of determinants [See Definition 4, here], we have:

det(A_(0R1)) = 0 [See Lemma Corollary 4.2, here]

(6) Using our previous results, we know that all det(E_i) ≠ 0. (See Lemma 4, Lemma 7, and Lemma 9 here)

(7) It therefore follows that det(A) = 0 since det(A_(0R1)) = det(E_n)det(E_n-1)...det(E₂)det(E₁)det(A)

QED

Corollary 1.1R: If A is a matrix with two identical rows, then det(A)=0

Proof:

(1) Let A be an n x m matrix where row i = row j and i ≠ j.

(2) We can define the set α_k such that:

if k = i, then α_k=1
if k = j, then α_k=-1
otherwise, α_k=0

(3) Clearly, α₁R₁ + ... + α_nR_n=0 where not all α_k = 0.

(4) Therefore, the rows of A of linearly dependent and using Lemma 1 above, det(A)=0.

QED

Lemma 1C:

If the columns of an n x n matrix A are linearly dependent, det(A)=0

Proof:

(1) Let A be an n x n matrix with columns that are linearly dependent.

[See Definition 1, here for review of linearly independent]

(2) Then, there exists α_i such that:

α₁C₁ + ... + α_nCn = 0.

(3) Then, it is possible to use elementary operations to set C₁ = 0 since:

(a) Multiply C₁ with α₁

(b) For each column i (where i = 2 .. n), add α_i*C_i to C₁.

(c) By step #2, it is clear after (a) and after each addition (b), C₁ = 0.

(4) So we have:

A_(0C1) = AE_nE_n-1...E₂E₁ where E_i is an elementary operation. [See Theorem 5, here for review of how elementary operations map to multiplication]

(5) Using the definition of determinants [See Definition 4, here], we have:

det(A_(0C1)) = 0 [See Lemma Corollary 4.2, here]

(6) Using our previous results, we know that all det(E_i) ≠ 0. (See Lemma 4, Lemma 7, and Lemma 9 here)

(7) It therefore follows that det(A) = 0 since det(A_(0C1)) = det(E_n)det(E_n-1)...det(E₂)det(E₁)det(A)

QED

Corollary 1.1C: If A is a matrix with two identical columns, then det(A)=0

Proof:

(1) Let A be an n x m matrix where row i = row j and i ≠ j.

(2) We can define the set α_k such that:

if k = i, then α_k=1
if k = j, then α_k=-1
otherwise, α_k=0

(3) Clearly, α₁R₁ + ... + α_nR_n=0 where not all α_k = 0.

(4) Therefore, the rows of A of linearly dependent and using Lemma 1 above, det(A)=0.

QED

Lemma 2: det(A) is a linear function of the rows of A

That is,

if three matrices A,B,C are exactly the same except for one row where this row is α for A, β for B, and (α + β) for C, then:

det(C) = det(A) + det(B)

Proof:

(1) Assume that the rows which are the same in A,B, and C are linearly dependent. [See Definition 1, here]

(2) Then det(A)=0, det(B)=0, and det(C)=0. [See Lemma 1 above]

(3) So that we have 0 = det(C) = det(A) + det(B) = 0 + 0

(4) Assume that all the rows but the first row are the same and that none of these rows are linearly dependent.

(5) Let F_{1 x n} be the set of all possible rows of length n.

(6) F_{1 x n} is a vector space. [See Definition 2, here for definition of vector space]

(7) Since [ R₂, R₃, ..., R_n ] are linearly independent, we can use this list to build a basis: [ ε, R₂, R₃, ..., R_n]. [See Theorem 1, here]

(8) Since [ ε, R₂, R₃, ..., R_n] is a basis (see Definition 2, here for definition of basis), we have:

Row₁(A) = α = a₁ε + a₂R₂ + ... + a_nR_n

Row₁(B) = β = b₁ε + b₂R₂ + ... + b_nR_n

Row₁(C) = (α + β) = (a₁ + b₁)ε + (a₂ + b₂)R₂ + ... + (a_n + b_n)R_n

(9) For A,B,C we can use I_{(kRj + Ri)} to simplify the first row [See Definition 3, here for definition of A_{(kRj + Ri)}].

For A, we set each k=a_i and then use R_i. In this way, we can reduce α to a₁*ε. Likewise, we can reduce β to b₁*ε and finally, we can reduce (α + β) to (a₁ + b₁)ε.

(10) Since det(AB) = det(A)det(B) [See Definition 4, here] and since det(I_{(kRj + Ri)} = 1 [See Lemma 7, here] , it follows that:

det(A) =



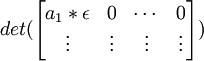
det(B) =



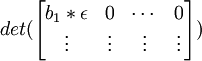
det(C) =



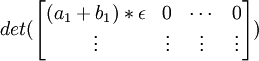
(11) It is also true that (see Definition 4, here):

det(A) =



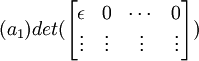
det(B) =



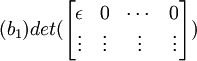
det(C) =



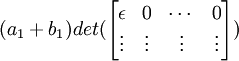
(12) And it is true that:

det(C) = det(A) + det(B)

(13) Now, we have one last case to deal with. In this case, A,B,C are all the same except for a row r that is not the first row and all other rows are linearly independent.

(14) Now, from the elementary operations (see Lemma 9, here), we know that:

det(A*I_{(Ri ↔ R1)}) = det(A)*(-1)

det(B*I_{(Ri ↔ R1)}) = det(B)*(-1)

det(C*I_{(Ri ↔ R1)}) = det(C)*(-1)

(15) Now from step #4 thru step #12, we know that:

det(C*I_{(Ri ↔ R1)}) = det(A*I_{(Ri ↔ R1)}) + det(B*I_{(Ri ↔ R1)}) =

= -det(C) = -det(A) + -det(B)

(16) Multiplying both sides by -1 gives us:

det(C) = det(A) + det(B)

QED

Corollary 2.1: det(A) is a linear function of the rows of A

That is,

if three matrices A,B,C are exactly the same except for one column where this row is α for A, β for B, and (α + β) for C, then:

det(C) = det(A) + det(B)

Proof:

(1) Using Lemma 2 above, we have:

det(C^T) = det(A^T) + det(B^T)

(2) Using Theorem 9 here, we have:

det(C^T) = det(C) det(A^T) = det(A)' det(B^T) = det (B)
(3) Putting this all together gives us:
det(C) = det(A) + det(B)

QED

Definition 1: Minor M_i,j(A)

For an n x n matrix A, the minor of a_i,j, M_i,j(A), is the n-1 x n-1 submatrix of A obtained by deleting row i and column j of A.

Definition 2: Cofactor

For an n x n matrix A, the cofactor of a_i,j, cof_i,j(A), is defined as (-1)^i+jdet(M_i,j(A)).

Lemma 3:

Let B be an F_{n x n} matrix of the form:



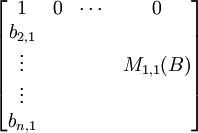
then:

det(B) = det(M_1,1(B)) = cof_1,1(B).

Proof:

(1) Using the elementary row operation I_{(kRj + Ri)} [See Definition 3, here] we can reduce B to the following form:



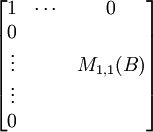
(2) Let E₁*....*E_t be a representation of M_1,1(B) as a product of n-1 x n-1 elementary matrices. [See Theorem 6, here]

(3) Now, we have:









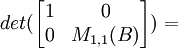
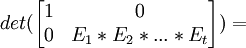
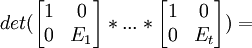
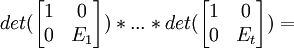
det(E₁)*...*det(E_t) = det(E₁*...*E_t) = det(M₁₁(B))

QED

Corollary 3.1:

Let B be an F_{n x n} matrix of the form:



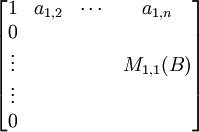
then:

det(B) = det(M_1,1(B)) = cof_1,1(B).

Proof:

(1) Using Lemma 3 above, we have:

det(B^T) = det(M_1,1(B)) = cof_1,1(B).

(2) Using Theorem 9 here, we have:

det(B) = det(B^T)

QED

Theorem 4: Cofactor Expansion of rows

The determinant of an n x n matrix can be computed as the sum of products of the elements of any row and their cofactors.

That is:

det(A) = ∑(j=1,n) a_i,jcof_i,j(A)

Proof:

(1) Let A be an n x n matrix.

(2) Let i be the row that we wish to use to compute det(A).

(3) Using Row operation II (I_{(Ri ↔ Rj)}), we move row i to row 1 by switching row i ↔ row (i-1) and row (i-1) ↔ row (i-2) ↔ ... ↔ row(2) ↔ row(1).

(4) We can see that there are i-1 such operations and at the end of it, we are left with the following order:



(5) Since det(I_{(Ri ↔ Rj)}) = -1, the (i-1) row operations gives us:





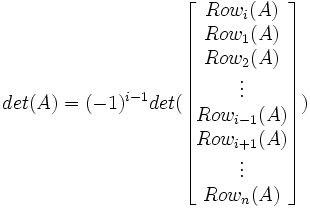
(6) Using Lemma 2 above, we have:
det(A) =



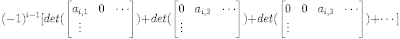
(7) Using Column Operation II, we can move the nonzero column at column j (where j represents the current column) to column 1. This consists of the same type of operation as before:

column i ↔ column (j-1) and column (j-1) ↔ column (j-2) ↔ ... ↔ column(2) ↔ column(1).

(8) This gives us (-1)⁰ for j=1, (-1)¹ for j=2, and so on so that we get:

det(A) = (-1)^(i-1)[(-1)^(1-1)det([a_i,1*]) + (-1)^(2-1)det([a_i,2*]) + ... + (-1)^(n-1)det([a_i,n*]) ]

where [a_i,j*] is the determinant of the [a_i,j] after it has been moved to column 1 using column operations.

(9) Since (-1) to an even number = 1 and (-1) to an odd number = -1, we can simplify step #8 to the following:

det(A) = (-1)^i-1[



]

(10) Using row operation I (I_(kRi)), we further get:

det(A) = (-1)^i-1[



]

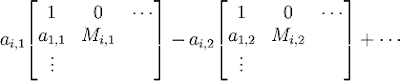
(11) We can now plug in Lemma 3 above to complete the proof:

det(A) =
(-1)^i-1[a_i,1det(M_i,1(A)) - a_i,2det(M_i,2(A)) + a_i,3det(M_i,3(A)) - a_i,4det(M_i,4(A)) + ...] =

(-1)^i-1[a_i,1cof_i,1(A) - a_i,2cof_i,2(A) + a_i,3cof_i,3(A) - a_i,4cof_i,4(A) + ... ]

QED

The implication of Theorem 4 is that we can now establish a recursive method for obtaining the determinant of an n x n matrix.

Algorithm 1: Find the determininant of any n x n matrix

(1) If n x n is a 2 x 2 matrix, then the determinant is:



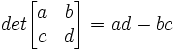
(2) If n x n is not a 2 x 2 matrix, then the determinant can be derived from the determinant of the Minor of n x n so that:

det(n x n) = a_1,1det(M_1,1) - a_1,2det(M_1,2) + ... + (-1)^(n-2)a_1,(n-1)det(M_1,(n-1) + (-1)^(n-1)a_1,ndet(M_1,n).

Corollary 4.1: Cofactor Expansion of columns

The determinant of an n x n matrix can be computed as the sum of products of the elements of any column and their cofactors.

That is:

det(A) = ∑(i=1,n) a_i,jcofactor_i,j(A)

Proof:

(1) Let A be an n x n matrix.

(2) Let j be the column that we wish to use to compute det(A).

(3) Using Column operation II (I_{(Ci ↔ Cj)}), we move column j to column 1 by switching column j ↔ column (j-1) and column (j-1) ↔ column (j-2) ↔ ... ↔ column(2) ↔ column(1).

(4) We can see that there are j-1 such operations and at the end of it, we are left with the following order:



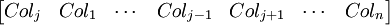
(5) Since det(I_{(Ci ↔ Cj)}) = -1,

det(A) = (-1)^(j-1)det([Col_j Col₁ ... Col_n])

(6) Using Corollary 2.1 above, we have:
det(A) = (-1)^(j-1)[det([a_1,j]) + det([a_2,j]) + ... + det([a_n,j])]

where [a_i,j] is the matrix derived from A where all values in column j are empty except for a_i,j.

(7) Using Row Operation II (I_{(Ri ↔ Rj)}), we can move this nonzero row at row i to row 1. This consists of the same type of operation as before:

row i ↔ row (i-1) and row (i-1) ↔ row (i-2) ↔ ... ↔ row(2) ↔ row(1).

(8) This gives us (-1)⁰ for i=1, (-1)¹ for i=2, and so on so that we get:

det(A) = (-1)^(j-1)[(-1)^(1-1)det([a_1,j*]) + (-1)^(2-1)det([a_2,j*]) + ... + (-1)^(n-1)det([a_n,j*]) ]

where [a_i,j*] is the determinant of the [a_i,j] after it has been moved to row 1 using row operations.

(9) Since (-1) to an even number = 1 and (-1) to an odd number = -1, we can simplify step #8 to the following:

det(A) = (-1)^(j-1)[det([a_1,j*]) - det([a_2,j*]) + ... {+/-} det([a_n,j*]) ]

where [a_i,j*] is the determinant of the [a_i,j] after it has been moved to row 1 using row operations.

(10) We can use column operation I (I_(kCi))to convert each matrix into this form:

det(A) = (-1)^(j-1)[a_1,jdet([a_i,j**]) - a_2,jdet([a_2,1**] + ... ]

where a_i,jdet([a_i,j**]) = det([a_i,j*])

(11) We can now plug in Corollary 3.1 above to complete the proof:

det(A) = (-1)^i-1[a_i,1det(M_i,1(A)) - a_i,2det(M_i,2(A)) + a_i,3det(M_i,3(A)) - a_i,4det(M_i,4(A)) + ...] =

(-1)^i-1[a_i,1cof_i,1(A) - a_i,2cof_i,2(A) + a_i,3cof_i,3(A) - a_i,4cof_i,4(A) + ... ]

QED

References

• Charles G. Cullen, Matrices and Linear Transformations, Dover Publications, Inc., 1972.