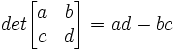
Math Refresher: Determinant of an n x n matrix

In a previous blog, I defined the determinant of a 2 x 2 matrix as:

In today's blog, I will offer a more general definition that is taken from Matrices and Linear Transformations by Charles G. Cullen.

Before offering this definition, I need to establish some notation for elementary operations of matrices. See here for review of these elementary operations.

Definition 1: A_{(kR_i)}

This is the matrix that results from multiplying a scalar k to the ith row of the matrix A.

Definition 2: A_{(R_i ↔ R_j)}

This is the matrix that results from interchanging row i with row j in the matrix A.

Definition 3: A_{(kR_j + R_i)}

This is the matrix that results from adding (a scalar k * row j) to row i in the matrix A.

Now, I can use these definitions to offer a more general definition of the determinant of an n x n matrix:

Definition 4: Determinant of an n x n matrix A det(A)

A function is said to be the determinant of an n x n matrix if:
(I) det(AB) = det(A)*det(B)
(II) det(I_(kR₁)) = k

NOTE: I_(kR₁) is the identity matrix I_n with k multiplied to row 1 in I. [See here for details on how modifying the identity matrix and how this relates to elementary operations.]

For example, I_(5R₁) =

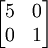
since for identity I₂:

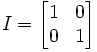
Now, from our previous result, we have shown that the above rule applies to 2 x 2 matrices.

Lemma 1: 2 x 2 matrices are determinants by Definition 4 above

Proof:

(1) Let A, B be 2 x 2 matrices.

(2) det(AB) = det(A)det(B) [See Lemma 1 here]

(3) I_(kR₁) =

(4) Using the definition of determinant for 2 x 2 matrices gives us:

k*1 - 0*0 = k

(5) Thus, we have shown that our proposed definition is consistent with the previous definition for 2 x 2 matrices.

QED

Lemma 2: I_{(kR_j)} = I_{(R_j ↔ R₁)}I_(kR₁)I_{(R_j ↔ R₁)}

Proof:

(1) I =

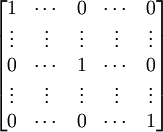
(2) I_{(R_j ↔ R₁)} =

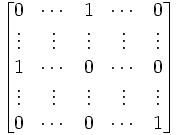
(3) I_(kR₁)I_{(R_j ↔ R₁)}

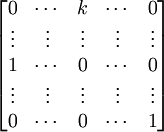
(4) I_{(R_j ↔ R₁)}I_(kR₁)I_{(R_j ↔ R₁)}

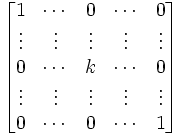
QED

Lemma 3: I_{(R_j ↔ R₁)}I_{(R_j ↔ R₁)} = I.

Proof:

(1) I =

(2) I_{(R_j ↔ R₁)} =

(3) I_{(R_j ↔ R₁)}I_{(R_j ↔ R₁)} =

QED

Lemma 4: det(I_{(kR_j)}) = k

Proof:

(1) det(I_{(kR_j)}) = det( I_{(R_j ↔ R₁)}I_(kR₁)I_{(R_j ↔ R₁)}) [See Lemma 2 above]

(2) det( I_{(R_j ↔ R₁)}I_(kR₁)I_{(R_j ↔ R₁)}) = det( I_{(R_j ↔ R₁)})det( I_(kR₁) )det( I_{(R_j ↔ R₁)}) [See Definition 4 above]

(3) det( I_{(R_j ↔ R₁)})det( I_(kR₁) )det( I_{(R_j ↔ R₁)}) = det( I_(kR₁) )det( I_{(R_j ↔ R₁)})det( I_{(R_j ↔ R₁)}) [from the Commutativity of scalars]

(4) det( I_(kR₁) )det( I_{(R_j ↔ R₁)})det( I_{(R_j ↔ R₁)}) = det( I_(kR₁) )det( I_{(R_j ↔ R₁)}I_{(R_j ↔ R₁)}) [ See Definition 4 above]

(5) det( I_(kR₁) )det( I_{(R_j ↔ R₁)}I_{(R_j ↔ R₁)}) = det( I_(kR₁) )det(I) [See Lemma 3 above]

(6) det( I_(kR₁) )det(I) = det(I_(kR₁))det(I_(1R₁))

(7) det( I_(kR₁))det(I_(1R₁)) = k*1 = k [See Definition 4 above]

QED

Corollary 4.1: A = I_{(kR_j)}B → det(A) = k*det(B)

Proof:

(1) A = I_{(kR_j)}B

(2) det(A) = det(I_{(kR_j)}B) = det(I_{(kR_j)})det(B) = k*det(B) [See Lemma 4 above]

QED

Corollary 4.2: det(I_{(0R_i)}) = 0

Proof:

(1) det(I_{(0R_i)}) = 0 [This follows directly from Lemma 4 above for k=0]

QED

Corollary 4.3: det(I) = 1

Proof:

(1) det(I) = det(I_{(1R_i)}) = 1. [This follows directly from Lemma 4 above for k = 1]

QED

Lemma 5: I_{(kR_j + R_i)} = I_{(k^-1R_j)}I_{(1R_j + R_i)}I_{(kR_j)}

Proof:

(1) I_{(kR_j + R_i)} =

(2) I_{(kR_j)}=

(3) I_{(1R_j + R_i)}I_{(kR_j)}=

(4) I_{(k^-1R_j)}I_{(1R_j + R_i)}I_{(kR_j)}=

QED

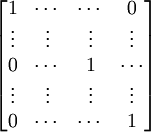
Lemma 6: I_{(k^-1R_j)}I_{(kR_j)} = I

Proof:

(1) I_{(kR_j)} =

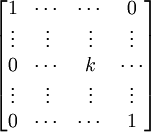
(2) I_{(k^-1R_j)}I_{(kR_j)} =

QED

Lemma 7: det(I_{(kR_j + R_i)}) = 1

Proof:

(1) Assume k = 0

(2) det(I_{(kR_j + R_i)}) = det(I_{(0R_j + R_i)}) = det(I) = det(I_(kR₁)) = 1 [See Definition 4 above]

(3) Assume k ≠ 0

(4) det(I_{(kR_j + R_i)}) =det( I_{(k^-1R_j)}I_{(1R_j + R_i)}I_{(kR_j)}) [See Lemma 5 above]

(5) det( I_{(k^-1R_j)}I_{(1R_j + R_i)}I_{(kR_j)}) = det( I_{(k^-1R_j)} )det( I_{(1R_j + R_i)} )det( I_{(kR_j)}) [See Definition 4 above]

(6) det( I_{(k^-1R_j)} )det( I_{(1R_j + R_i)} )det( I_{(kR_j)}) = det( I_{(1R_j + R_i)} )det( I_{(k^-1R_j)} )det( I_{(kR_j)}) [from the Commutativity of scalars]

(7) det( I_{(1R_j + R_i)} )det( I_{(k^-1R_j)} )det( I_{(kR_j)}) = det( I_{(1R_j + R_i)} )det( I_{(k^-1R_j)} I_{(kR_j)}) [see Definition 4 above]

(8) det( I_{(1R_j + R_i)} )det( I_{(k^-1R_j)} I_{(kR_j)}) = det( I_{(1R_j + R_i)} )det( I ) [See Lemma 6 above]

(9) det( I_{(1R_j + R_i)} )det( I ) = det( I_{(1R_j + R_i)} I) = det(I_{(1R_j + R_i)}) [See Definition 4 above]

(10) So, we have shown that: det(I_{(kR_j + R_i)}) = det(I_{(1R_j + R_i)})

(11) Now, (I_{(1R_j + R_i)})² = (I_{(1R_j + R_i)})(I_{(1R_j + R_i)}) = I_{(2R_j + R_i)}

(12) But for k=2, we have:

det( (I_{(1R_j + R_i)})(I_{(1R_j + R_i)})) = det(I_{(2R_j + R_i)} ) = det(I_{(1R_j + R_i)})

(13) Now, this can only be true if det(I_{(1R_j + R_i)}) = 0 or det(I_{(1R_j + R_i)}) = 1.

(14) We note that I_{(1R_j + R_i)}I_{(-1R_j + R_i)} = I.

(15) Since det(I) = 1, it follows that det(I_{(1R_j + R_i)}I_{(-1R_j + R_i)}) = 1 so it is impossible for det(I_{(1R_j + R_i)}) = 0.

(16) Therefore, det(I_{(1R_j + R_i)}) = 1.

QED

Corollary 7.1: A = I_{(kR_j + R_i)}B → det(A) = det(B)

Proof:

(1) A = I_{(kR_j + R_i)}B

(2) det(A) = det(I_{(kR_j + R_i)}B) = det(I_{(kR_j + R_i)})det(B) = 1*det(B) = det(B) [See Lemma 7 above]

QED

Lemma 8: I_{(R_i ↔ R_j)} = I_{(-R_i)}I_{(1R_i + R_j)}I_{(-R_j + R_i)}I_{(1R_i + R_j)}

Proof:

(1) I_{(R_i ↔ R_j)} =

(2) I_{(1R_i + R_j)} =

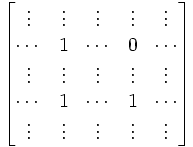
(3) I_{(-R_j + R_i)}I_{(1R_i + R_j)}=

(4) I_{(1R_i + R_j)}I_{(-R_j + R_i)}I_{(1R_i + R_j)} =

(5) I_{(-R_i)}I_{(1R_i + R_j)}I_{(-R_j + R_i)}I_{(1R_i + R_j)}=

QED

Lemma 9: det(I_{(R_i ↔ R_j)}) = -1.

Proof:

(1) det( I_{(R_i ↔ R_j)} ) = det( I_{(-R_i)}I_{(1R_i + R_j)}I_{(-R_j + R_i)}I_{(1R_i + R_j)}) [See Lemma 8 above]

(2) det( I_{(-R_i)}I_{(1R_i + R_j)}I_{(-R_j + R_i)}I_{(1R_i + R_j)}) = det( I_{(-R_i)} )det( I_{(1R_i + R_j)} )det( I_{(-R_j + R_i)})det( I_{(1R_i + R_j)}) [See Definition 4 above]

(3) det( I_{(-R_i)} ) = -1 [See Lemma 4 above]

(4) det( I_{(1R_i + R_j)} ) = det( I_{(-R_j + R_i)}) = 1 [See Lemma 7 above]

(5) So, det( I_{(-R_i)} )det( I_{(1R_i + R_j)} )det( I_{(-R_j + R_i)})det( I_{(1R_i + R_j)}) = (-1)*(1)*(1)*(1) = -1.

QED

Corollary 9.1: A =I_{(R_i ↔ R_j)}B → det(A) = -det(B).

Proof:

(1) A =I_{(R_i ↔ R_j)}B

(2) det(A) = det(I_{(R_i ↔ R_j)}B) = det(I_{(R_i ↔ R_j)})det(B) = (-1)*det(B) = -det(B)

QED

Lemma 10:

Let E_i be an elementary matrix

Let A =

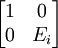
then:

det(A) = det(E_i)

Proof:

(1) There are only three types of elementary matrices so this proof is complete if I show it is true for each type.

(2) Type I: E_i = I_{(kR_i)}

(a) From Lemma 4 above, det(E_i) = k

(b) A, in this case, is equal to I_{(kR_i+1)}

(c) Using Lemma 4 above, det(A) = k

(3) Type II: E_i = I_{(kR_j + R_i)}

(a) From Lemma 7 above, det(E_i) = 1

(b) A, in this case, is equal to I_{(kR_j+1 + R_i+1)}

(c) Using Lemma 7 above, det(A) = 1.

(4) Type III: E_i = I_{(R_i ↔ R_j)}

(a) From Lemma 9 above, det(E_i) = -1.

(b) A, in this case, is equal to I_{(R_i+1 ↔ R_j+1)}

(c) Using Lemma 9 above, det(A) = -1

QED

References

Charles G. Cullen, Matrices and Linear Transformations, Dover Publications, Inc., 1972.

Math Refresher

Thursday, June 07, 2007

Determinant of an n x n matrix

No comments :

About Me

Blog Archive