Integral Test for Infinite Series

The Integral Test for Infinite Series is a well known convergence test that uses integrals. The Integral Test, for example, can be used, for example, to show that the harmonic series diverges (that is, does not have a limit).

The content in today's blog is taken from Edwards and Penney, Calculus and Analytic Geometry.

Definition 1: Improper Integral

An Improper Integral is an integral on an interval that is open (does not include its endpoints) or on a closed interval that is unbounded (that is, one of its endpoints is either ∞ or -∞). [See here for a review of open and closed intervals]

Improper integrals are used to analyze infinite series. The improper integral is the limit of a sequence of definite integrals where endpoints get closer and closer to the limit.

Theorem 1: The Integral Test

Let ∑ a_n be a positive-term series (none of the elements are negative) and let f(x) be a function that is a positive valued, decreasing continuous function for x ≥ 1.

If f(n) = a_n for all integers n ≥ 1, then the series and the improper integral:

∑ (n=1, ∞) a_n

∫ (1,∞) f(x)dx

either both converge or diverge. That is, one diverges if and only if the other diverges.

Proof:

(1) Let S_n = a₁ + a₂ + ... + a_n

(2) If f(n) = a_n for all integers n ≥ 1, then it is clear that for the region under y=f(x) from x=1 to x = n+1:

∫ (1,n+1) f(x)dx ≤ S_n (see graph below)

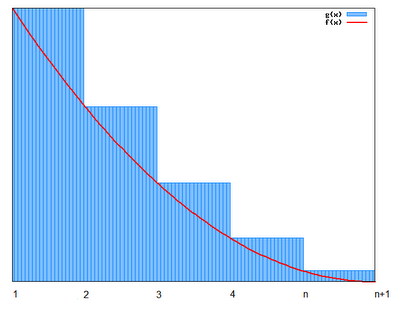(3) If we now consider the sum S_n - a₁ = a₂ + a₃ + ... + a_n, then:

If f(n) = a_n for all integers n ≥ 1, then it is clear that for the region under y=f(x) from x=1 to x = n:

S_n - a₁ ≤ ∫ (n,1) f(x)dx (see graph below)

(4) Assume that ∫(∞,1) f(x)dx diverges.

Then it goes to +∞ since by assumption f(x) is a positive term series.

(5) lim (n → ∞) ∫ (n+1,1) f(x) = +∞

(6) From step #2, it is clear that lim (n → ∞) Sn = +∞ so that ∑ a_n diverges.

(7) Assume that ∫(∞,1) f(x)dx converges with value = I.

(8) From step #3,

S_n ≤ a₁ + ∫(n,1)f(x)dx ≤ a₁ + I

(9) So the monotone increasing sequence {S_n} (∞,1) is bounded. [See Definition 8, here for definition of monotone increasing sequence, see Definition 4, here for definition of bounded]

(10) This gives that the infinite series ∑ a_n = lim (n → ∞) S_n converges also.

QED

Corollary 1.1: Harmonic series diverges

∑ (n=1, ∞) 1/n = 1 + 1/2 + 1/3 + 1/4 + ...

Proof:

(1) f(x)=1/x is positive, continuous, and decreasing for x ≥ 1.

(2) ∫(∞,1) (1/x)dx = lim (b → ∞) ∫ (b,1) (1/x)dx = lim (b → ∞) [ln x] (b,1) [This follows from the derivative of 1/x, see Lemma 1, here]

(3) lim (b → ∞) [ln x] (b,1) = lim (b → 0) (ln b - ln 1) = + ∞

(4) Therefore, using the Integral Test above, the series diverges.

QED

Corollary 1.2: Zeta function converges if s > 1 but diverges if 0 is less than s ≤ 1.

ζ(s) = ∑ (n=1,∞) 1/n^s = 1 + 1/2^s + 1/3^s + ... + 1/n^s + ...

Proof:

(1) The case where s=1 was proven in Corollary 1.1

(2) If s is greater than 0 and s ≠ 1, then f(x) = 1/x^s satisfies the conditions of the integral test (it is a positive-valued, decreasing, continuous function for x ≥ 1).

(3) ∫ (∞,1) (1/x^s)dx = lim (b → ∞) ∫ (b,1) (1/x^s)dx = lim (b → ∞) [-1/[(s-1)x^s-1]] (b,1) [This follows from the power rule for derivatives (see Lemma 2, here) and the fundamental theorem of calculus]

(4) lim (b → ∞) [-1/[(s-1)x^s-1]] (b,1) = lim(b → ∞) (1/[s-1])[1 - 1/(b^s-1)]

(5) If s is greater than 1, then:

lim(b → ∞) (1/[s-1])[1 - 1/(b^s-1)] = (1/[s-1])(1) = (1/[s-1]) which is less than ∞ so it converges.

(6) If 0 is less than s is less than 1, then:

∫ (∞,1)(1/x^s)dx = lim (b → ∞) [1/(1-s)](b^1-p - 1) = ∞

[This follows from the generalized power rule for derivatives (see Theorem, here) and the fundamental theorem of calculus]

(7) The conclusion follows from the Integral Test above.

QED

References

• Mohamed A. Khamsi, "Improper Integrals: An Introduction", SOSMath.com
• Edwards & Penney, Calculus and Analytic Geometry